如图，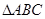
在平面
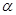内，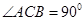
，AB=2BC=2，P为平面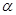外一个动点，且PC=
，
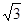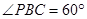
（1）问当PA的长为多少时，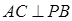
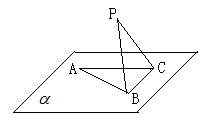
（2）当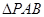
的面积取得最大值时，求直线PC与平面PAB所成角的正弦值
已知函数
为自然对数的底数）．
（1）求曲线
在
处的切线方程；
（2）若
是
的一个极值点，且点
，
满足条件：
.
（ⅰ）求的值；
（ⅱ）求证：点
，
，
是三个不同的点，且构成直角三角形．
设向量
，定义一种向量积
．
已知向量
，
，点
为
的图象上的动点，点
为
的图象上的动点，且满足
（其中
为坐标原点）．
（1）请用
表示
；
（2）求的表达式并求它的周期；
（3）把函数图象上各点的横坐标缩小为原来的
倍（纵坐标不变），得到函数
的图象.设函数
，试讨论函数
在区间
内的零点个数.
（已知抛物线
（
）的准线与
轴交于点
．
（1）求抛物线的方程，并写出焦点坐标；
（2）是否存在过焦点的直线
（直线与抛物线交于点
，
），使得三角形
的面积
？若存在，请求出直线的方程；若不存在，请说明理由．
如图，在三棱锥
中，平面
平面
，
于点
，且
，
，
（1）求证：
（2）
（3）若
，
，求三棱锥的体积．
将数列
按如图所示的规律排成一个三角形数表，并同时满足以下两个条件：①各行的第一
个数
构成公差为
的等差数列；②从第二行起，每行各数按从左到右的顺序都构成公比为
的等比数列.若
，
，
.
（1）求
的值；
（2）求第
行各数的和
.