(已知抛物线 (
( )的准线与
)的准线与 轴交于点
轴交于点 .
.
(1)求抛物线的方程,并写出焦点坐标;
(2)是否存在过焦点的直线 (直线与抛物线交于点
(直线与抛物线交于点 ,
, ),使得三角形
),使得三角形 的面积
的面积 ?若存在,请求出直线
?若存在,请求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
已知三棱锥 的底面
的底面 是直角三角形,且
是直角三角形,且 ,
, 平面
平面 ,
, ,
, 是线段
是线段 的中点,如图所示.
的中点,如图所示.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)求三棱锥 的体积.
的体积.
2000辆汽车通过某一段公路时的时速的频率分布直方图如图所示. 问;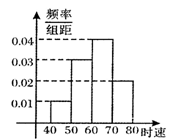
(Ⅰ)时速在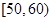 的汽车大约有多少辆?
的汽车大约有多少辆?
(Ⅱ)如果每个时段取中值来代表这个时段的平均速度,如时速在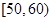 的汽车其速度视为55,请估算出这2000辆汽车的平均速度.
的汽车其速度视为55,请估算出这2000辆汽车的平均速度.
在公差不为0的等差数列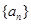 中,
中,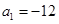 ,且
,且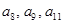 依次成等差数列.
依次成等差数列.
(Ⅰ)求数列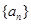 的公差;
的公差;
(Ⅱ)设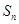 为数列
为数列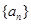 的前
的前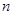 项和,求
项和,求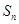 的最小值,并求出此时的
的最小值,并求出此时的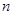 值
值
设向量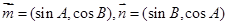
 且
且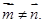 其中
其中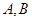 是
是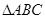 的内角.
的内角.
(Ⅰ)求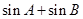 的取值范围;
的取值范围;
(Ⅱ)试确定 的取值范围.
的取值范围.
已知函数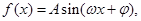
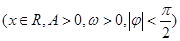 的部分图象如图所示:
的部分图象如图所示: 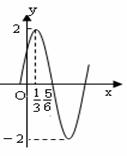
(Ⅰ)试确定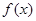 的解析式;
的解析式;
(Ⅱ)若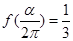 , 求
, 求 的值.
的值.