已知椭圆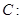
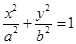
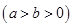 的左右焦点分别是
的左右焦点分别是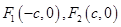 ,直线
,直线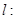
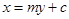 与椭圆
与椭圆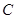 交于两点
交于两点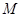 ,
,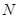 .当
.当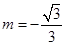 时,M恰为椭圆
时,M恰为椭圆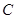 的上顶点,此时△
的上顶点,此时△ 的周长为6.
的周长为6.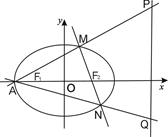
(Ⅰ)求椭圆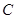 的方程;
的方程;
(Ⅱ)设椭圆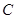 的左顶点为A,直线
的左顶点为A,直线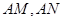 与直线
与直线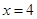 分别相交于点
分别相交于点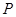 ,
,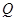 ,问当
,问当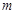
变化时,以线段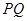 为直径的圆被
为直径的圆被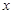 轴截得的弦长是否为定值?若是,求出这个定值,
轴截得的弦长是否为定值?若是,求出这个定值,
若不是,说明理由.
2013年某工厂生产某种产品,每日的成本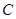 (单位:万元)与日产量
(单位:万元)与日产量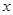 (单位:吨)满足函数关系式
(单位:吨)满足函数关系式 ,每日的销售额
,每日的销售额 (单位:万元)与日产量
(单位:万元)与日产量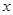 的函数关系式
的函数关系式
已知每日的利润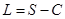 ,且当
,且当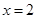 时,
时,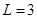 .
.
(1)求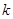 的值;
的值;
(2)当日产量为多少吨时,每日的利润可以达到最大,并求出最大值.
某食品厂为了检查甲乙两条自动包装流水线的生产情况,随即在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在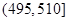 的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.
的产品为合格品,否则为不合格品.表1是甲流水线样本频数分布表,图1是乙流水线样本的频率分布直方图.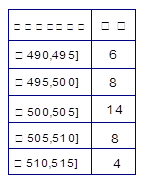

表1:(甲流水线样本频数分布表) 图1:(乙流水线样本频率分布直方图)
(1)根据上表数据在答题卡上作出甲流水线样本的频率分布直方图;
(2)若以频率作为概率,试估计从两条流水线分别任取1件产品,该产品恰好是合格品的概率分别是多少;
(3)由以上统计数据完成下面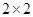 列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
列联表,并回答有多大的把握认为“产品的包装质量与两条自动包装流水线的选择有关”.
| 甲流水线 |
乙流水线 |
合计 |
|
| 合格品 |
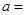 |
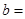 |
|
| 不合格品 |
 |
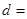 |
|
| 合 计 |
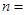 |
附:下面的临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
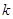 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: ,其中
,其中 )
)
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4, BD= ,AB=2CD=8.
,AB=2CD=8.
(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)求四棱锥P-ABCD的体积.
设向量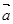 =
=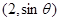 ,
,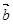 =
=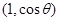 ,
,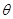 为锐角.
为锐角.
(1)若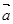 ∥
∥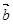 ,求tanθ的值;
,求tanθ的值;
(2)若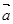 ·
·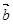 =
=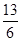 ,求sin
,求sin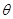 +cos
+cos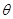 的值.
的值.
已知椭圆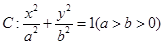 的左右焦点分别为
的左右焦点分别为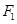 、
、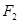 ,离心率
,离心率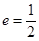 ,直线
,直线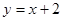 经过左焦点
经过左焦点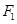 .
.
(1)求椭圆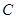 的方程;
的方程;
(2)若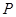 为椭圆
为椭圆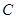 上的点,求
上的点,求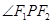 的范围.
的范围.