已知函数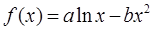 图象上一点
图象上一点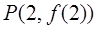 处
处
的切线方程为y= -3x+2ln2+2.
(1)求a,b的值;
(2)若方程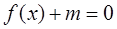 在
在 内有两个不等实根,求m的取值范围(其
内有两个不等实根,求m的取值范围(其
中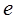 为自然对数的底数);
为自然对数的底数);
(本小题满分13分)(理科做)在如图所示的多面体中,底面BCFE是梯形,EF//BC,又EF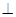 平面AEB,AE
平面AEB,AE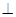 EB,AD//EF,BC=2AD=4,EF=3,AE=BE=2,G为BC的中点.
EB,AD//EF,BC=2AD=4,EF=3,AE=BE=2,G为BC的中点.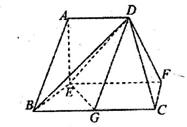
(1)求证:AB//平面DEG;
(2)求证:BD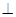 EG;
EG;
(3)求二面角C—DF—E的正弦值.
(文科做)已知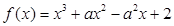 .
.
(1)若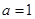 ,求曲线
,求曲线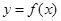 在点
在点 处的切线方程;
处的切线方程;
(2)若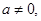 求函数
求函数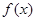 的单调区间.
的单调区间.
(本小题满分8分)已知圆C: ,直线
,直线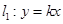 与圆C交于P、Q两个不同的点,M为P、Q的中点.
与圆C交于P、Q两个不同的点,M为P、Q的中点.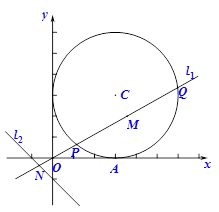
(Ⅰ)已知 ,若
,若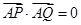 ,求实数
,求实数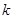 的值;
的值;
(Ⅱ)求点M的轨迹方程;
(本小题满分10分)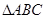 中
中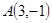 ,
,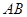 边上的中线
边上的中线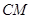 所在直线方程为
所在直线方程为 ,
,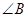 的平分线方程
的平分线方程 为
为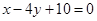 .
.
(1)求顶点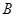 的坐标;
的坐标;
(2)求直线 的方程.
的方程.
(本小題满分16分)已知椭圆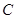 :
: 的焦距为
的焦距为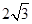 ,离心率为
,离心率为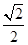 ,其右焦点为
,其右焦点为 ,过点
,过点 作直线交椭圆于另一点
作直线交椭圆于另一点 .
.
(1)若 ,求
,求 外接圆的方程;
外接圆的方程;
(2)若过点 的直线与椭圆
的直线与椭圆
 相交于两点
相交于两点 、
、 ,设
,设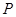 为
为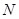 上一点,且满足
上一点,且满足 (
( 为坐标原点),当
为坐标原点),当 时,求实数
时,求实数 的取值范围.
的取值范围.
(本小题满分16分)(理科做)已知四棱锥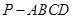 的底面为直角梯形,
的底面为直角梯形, ,
,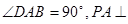 底面
底面 ,且
,且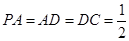 ,
, ,
,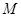 是
是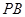 的中点。
的中点。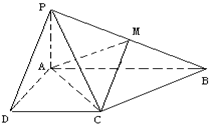
(1)证明:面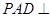 面
面 ;
;
(2)求 与
与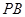 所成的角的余弦值;
所成的角的余弦值;
(3)求面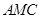 与面
与面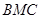 所成二面角的余弦值.
所成二面角的余弦值.
(文科做)已知函数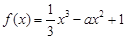 .
.
(1)若函数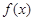 的图象关于点
的图象关于点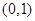 对称,直接写出
对称,直接写出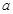 的值;
的值;
(2)求函数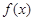 的单调递减区间;
的单调递减区间;
(3)若 在区间
在区间 上恒成立,求
上恒成立,求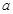 的最大值.
的最大值.