设函数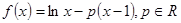 .
.
(Ⅰ)当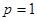 时,求函数
时,求函数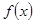 的单调区间;
的单调区间;
(Ⅱ)设函数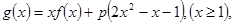 求证:当
求证:当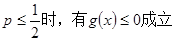
已知函数f(x)=x2+xsinx+cosx.
(1)若曲线y=f(x)在点(a,f(a))处与直线y=b相切,求a与b的值;
(2)若曲线y=f(x)与直线y=b有两个不同交点,求b的取值范围.
某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12 000π元(π为圆周率).
(1)将V表示成r的函数V(r),并求该函数的定义域;
(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.
已知函数f(x)=x-aln x(a∈R).
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求函数f(x)的极值.
已知函数f(x)=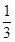 x3+
x3+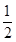 ax2+bx.
ax2+bx.
(1)若a=2b,试问函数f(x)能否在x=-1处取到极值?若有可能,求出实数a,b的值;否则说明理由.
(2)若函数f(x)在区间(-1,2),(2,3)内各有一个极值点,试求w=a-4b的取值范围.
某化工企业2012年底投入100万元购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.设该企业使用该设备x年的年平均污水处理费用为y(单元:万元).
(1)用x表示y;
(2)当该企业的年平均污水处理费用最低时,企业需重新更换新的污水处理设备.求该企业几年后需要重新更换新的污水处理设备.