某冰箱厂为响应国家“家电下乡”号召,计划生产 、
、 两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于 4.75万元,不高于4.8万元,两种型号的冰箱生产成本和售价如下表:
两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于 4.75万元,不高于4.8万元,两种型号的冰箱生产成本和售价如下表:
| 型号 |
A型 |
B型 |
| 成本(元/台) |
2200 |
2600 |
| 售价(元/台) |
2800 |
3000 |
(1)冰箱厂有哪几种生产方案?
(2)该冰箱厂按哪种方案生产,才能使投入成本最少?“家电下乡”后农民买家电(冰箱、彩电、洗衣机)可享受13%的政府补贴,那么在这种方案下政府需补贴给农民多少元?
(3)若按(2)中的方案生产,冰箱厂计划将获得的全部利润购买三种物品:体育器材、实验设备、办公用品支援某希望小学.其中体育器材至多买4套,体育器材每套6000元,实验设备每套3000元,办公用品每套1800元,把钱全部用尽且三种物品都购买的情况下,请你直接写出实验设备的买法共有多少种.
如图,已知正比例函数和反比例函数的图象都经过点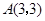 .
.求正比例函数和反比例函数的解析式;
把直线OA向下平移后与反比例函数的图象交于点
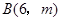 ,求
,求 的值和这个一次函数的解析式;
的值和这个一次函数的解析式;第(2)问中的一次函数的图象与
 轴、
轴、 轴分别交于C、D,求过A、B、D三点的二次函数的解析式;
轴分别交于C、D,求过A、B、D三点的二次函数的解析式;在第(3)问的条件下,二次函数的图象上是否存在点E,使四边形OECD的面积
 与四边形OABD的面积S满足:
与四边形OABD的面积S满足: ?若存在,求点E的坐标;若不存在,请说明理由.
?若存在,求点E的坐标;若不存在,请说明理由.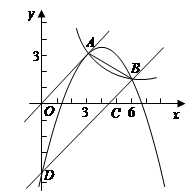
某电视机生产厂家去年销往农村的某品牌电视机每台的售价y(元)与月份x之间满足函数关系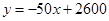 ,去年的月销售量p(万台)与月份x之间成一次函数关系,其中两个月的销售情况如下表:
,去年的月销售量p(万台)与月份x之间成一次函数关系,其中两个月的销售情况如下表:
求该品牌电视机在去年哪个月销往农村的销售金额最大?最大是多少?
)由于受国际金融危机的影响,今年1、2月份该品牌电视机销往农村的售价都比去年12月份下降了
 ,且每月的销售量都比去年12月份下降了1.5m%.国家实施“家电下乡”政策,即对农村家庭购买新的家电产品,国家按该产品售价的13%给予财政补贴.受此政策的影响,今年3至5月份,该厂家销往农村的这种电视机在保持今年2月份的售价不变的情况下,平均每月的销售量比今年2月份增加了1.5万台.若今年3至5月份国家对这种电视机的销售共给予了财政补贴936万元,求
,且每月的销售量都比去年12月份下降了1.5m%.国家实施“家电下乡”政策,即对农村家庭购买新的家电产品,国家按该产品售价的13%给予财政补贴.受此政策的影响,今年3至5月份,该厂家销往农村的这种电视机在保持今年2月份的售价不变的情况下,平均每月的销售量比今年2月份增加了1.5万台.若今年3至5月份国家对这种电视机的销售共给予了财政补贴936万元,求 的值(保留一位小数).
的值(保留一位小数).
(参考数据: ,
,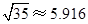 ,
, ,
, )
)
如图,已知:等边三角形 的边长为6,点
的边长为6,点 、
、 分别在边
分别在边 、
、 上,且
上,且 . 点
. 点 从点
从点 开始以每秒1个单位长的速度沿射线
开始以每秒1个单位长的速度沿射线 方向运动,设点
方向运动,设点 运动的时间为
运动的时间为 秒. 当
秒. 当 时,直线
时,直线 与过点
与过点 且平行于
且平行于 的直线相交于点
的直线相交于点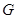 ,
, 的延长线与
的延长线与 的延长线相交于点
的延长线相交于点 ,
, 与
与 相交于点
相交于点
用
 的代数式表示
的代数式表示 ;
;设△
 的面积为
的面积为 ,写出
,写出 与
与 的函数关系式;
的函数关系式;当
 为何值时,点
为何值时,点 和点
和点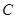 是线段
是线段 的三等分点?
的三等分点?
某校九年级共有200名女生在初中毕业生升学体育集中测试的速度类项目中选择了立定跳远,现从这200名女生中随机抽取10名女生进行测试,下面是她们测试结果的条形图.(另附:九年级女生立定跳远的计分标准)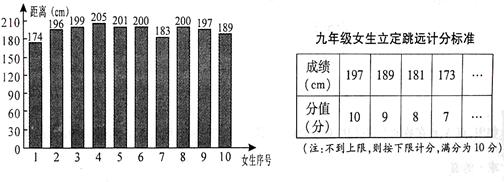
求这10名女生在本次测试中,立定跳远距离的极差,立定跳远得分的众数和平均数.
请你估计该校选择立定跳远的200名女生得满分的人数.
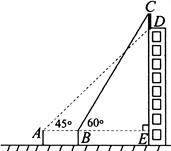
如图,某电视台大楼顶部安置了一电视发射铁塔CD,现有一位测试员分别在楼下相距16m的A,B两处测得D点和C点的仰角分别是45°和60°,已知A,B,E在一条直线上,C,D,E也在一条直线上,且BE=30m.求电视发射铁塔的高度.(结果保留整数,参考数据:≈1.41,≈1.73)