如图,正三棱柱ABC—A1B1C1的底面边长的3,侧棱AA1=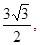 D是CB延长线上一点,且BD=BC.
D是CB延长线上一点,且BD=BC.
(Ⅰ)求证:直线BC1//平面AB1D;
(Ⅱ)求二面角B1—AD—B的大小;
(Ⅲ)求三棱锥C1—ABB1的体积.
到银行办理个人异地汇款(不超过100万)时,银行要收取一定的手续费.汇款额不超过100元,收取1元手续费;超过100元但不超过5000元,按汇款额的1%收取;超过5000元,一律收取50元手续费.试用条件语句描述汇款额为x元时,银行收取的手续费为y元的过程,画出程序框图并写出程序.
给出如下程序.(其中x满足:0<x<12)
程序: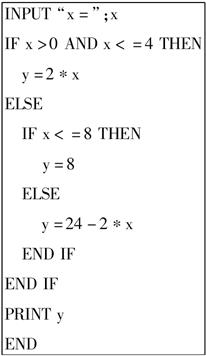
(1)该程序用函数关系式怎样表达.
(2)画出这个程序的程序框图.
输入一个数x,如果它是正数,则输出它;否则不输出.画出解决该问题的程序框图,并写出对应的程序.
已知函数f(x)=3x-1,求f[f(2)]的值,设计一个程序,解决上述问题.
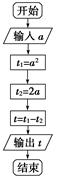
根据如图所示的程序框图,将算法语句改写为程序.