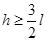中子星是恒星演化过程中的一种可能结果,它的密度很大.现有一中子星,观测到
它的自转周期为T=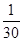 s.问该中子星的最小密度应是多少才能维持该星体的稳定,不
s.问该中子星的最小密度应是多少才能维持该星体的稳定,不
致因自转而瓦解?(计算时星体可视为均匀球体,万有引力常量G=6.67×10-11m3/(kg·s2))
在水平地面上有一个质量为4kg的物体,物体在水平拉力F的作用下由静止开始运动。10s末拉力减为 F该物体的v-t,图象如图所示。求:
F该物体的v-t,图象如图所示。求: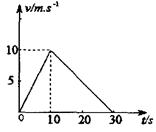
物体受到的水平拉力F的大小
物体与地面间的动摩擦因数。(g=10m/s2
如图所示,质量为20kg的物体放在水平地面上,已知物体与水平地面间的动摩擦因数为0.3。现给物体施加一个与水平面成370角的斜向上的拉力F=50N的作用,则物体受到的摩擦力多大?(设最大静摩擦力和滑动摩擦力相等,取g= 10m/s2,sin370 =" 0.6" ,cos370 = 0.8)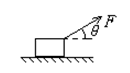
如图所示,用一根绳子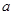 把物体挂起来,再用一根水平的绳子
把物体挂起来,再用一根水平的绳子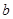 把物体拉向一旁固定起来. 物体的重量是40N,绳子
把物体拉向一旁固定起来. 物体的重量是40N,绳子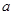 与竖直方向的夹角
与竖直方向的夹角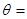 30°,绳子
30°,绳子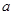 和
和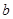 对物体的拉力分别是多大?
对物体的拉力分别是多大?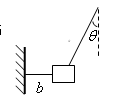
在粗糙水平轨道上,有一物块以初速度v0=6m/s,向右做匀减速直线运动,其加速度a大小为4m/s2,求:物块运动了多长时间速度为零;
物块运动的前0.5s内位移的大小。
如图所示,一不可伸长的轻质细绳,绳长为L一端固定于O点,另一端系一质量为m的小球,小球绕O点在竖直平面内做圆周运动(不计空气助力),小球通过最低点时的速度为v。求小球通过最低点时,绳对小球拉力F的大小;
若小球运动到最低点或最高点时,绳突然断开,两种情况下小球从抛出到落地水平位移大小相等,求O点距地面的高度h;
在(2)中所述情况下试证明O点距离地面高度h与绳长l之间应满足