下表给出1980年至今的百米世界记录情况:
| 国籍 |
姓名 |
成绩(秒) |
日期 |
国籍 |
姓名 |
成绩(秒) |
日期 |
| 牙买加 |
博尔特 |
9.72 |
2008.6.1 |
美国 |
格林 |
9.79 |
1999.6.16 |
| 牙买加 |
鲍威尔 |
9.74 |
2007.9.9 |
加拿大 |
贝利 |
9.84 |
1996.7.27 |
| 牙买加 |
鲍威尔 |
9.77 |
2006.8.18 |
美国 |
伯勒尔 |
9.85 |
1994.6.7 |
| 牙买加 |
鲍威尔 |
9.77 |
2006.6.11 |
美国 |
刘易斯 |
9.86 |
1991.8.25 |
| 美国 |
加特林 |
9.77 |
2006.5.12 |
美国 |
伯勒尔 |
9.90 |
1991.6.14 |
| 牙买加 |
鲍威尔 |
9.77 |
2005.6.14 |
美国 |
刘易斯 |
9.92 |
1988.9.24 |
| 美国 |
蒙哥 马利 |
9.78 |
2002.9.14 |
美国 |
史密斯 |
9.93 |
1983.7.3 |
(1)请你根据以上成绩数据,求出该组数据的众数为 ,极差为 .
(2)请在下图中用折线图描述此组数据.
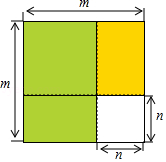
如图,将边长为 的正方形纸板沿虚线剪成两个小正方形和两个矩形,拿掉边长为 的小正方形纸板后,将剩下的三块拼成新的矩形.
(1)用含 或 的代数式表示拼成矩形的周长;
(2) , ,求拼成矩形的面积.
在6.26国际禁毒日到来之际,贵阳市教育局为了普及禁毒知识,提高禁毒意识,举办了“关爱生命,拒绝毒品”的知识竞赛.某校初一、初二年级分别有300人,现从中各随机抽取20名同学的测试成绩进行调查分析,成绩如下:
|
初一: |
68 |
88 |
100 |
100 |
79 |
94 |
89 |
85 |
100 |
88 |
|
100 |
90 |
98 |
97 |
77 |
94 |
96 |
100 |
92 |
67 |
|
|
初二: |
69 |
97 |
96 |
89 |
98 |
100 |
99 |
100 |
95 |
100 |
|
99 |
69 |
97 |
100 |
99 |
94 |
79 |
99 |
98 |
79 |
(1)根据上述数据,将下列表格补充完成.
整理、描述数据:
|
分数段 |
|
|
|
|
|
初一人数 |
2 |
2 |
4 |
12 |
|
初二人数 |
2 |
2 |
1 |
15 |
分析数据:样本数据的平均数、中位数、满分率如表:
|
年级 |
平均数 |
中位数 |
满分率 |
|
初一 |
90.1 |
93 |
|
|
初二 |
92.8 |
|
|
得出结论:
(2)估计该校初一、初二年级学生在本次测试成绩中可以得到满分的人数共 人;
(3)你认为哪个年级掌握禁毒知识的总体水平较好,说明理由.
如图,以 为顶点的抛物线 交 轴于 、 两点,交 轴于点 ,直线 的表达式为 .
(1)求抛物线的表达式;
(2)在直线 上有一点 ,使 的值最小,求点 的坐标;
(3)在 轴上是否存在一点 ,使得以 、 、 为顶点的三角形与 相似?若存在,请求出点 的坐标;若不存在,请说明理由.

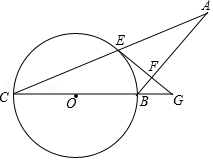
如图,在 中,以 为直径的 交 于点 ,过点 作 的垂线交 于点 ,交 的延长线于点 ,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径.
某商店销售一款进价为每件40元的护肤品,调查发现,销售单价不低于40元且不高于80元时,该商品的日销售量 (件 与销售单价 (元 之间存在一次函数关系,当销售单价为44元时,日销售量为72件;当销售单价为48元时,日销售量为64件.
(1)求 与 之间的函数关系式;
(2)设该护肤品的日销售利润为 (元 ,当销售单价 为多少时,日销售利润 最大,最大日销售利润是多少?