已知双曲线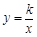
与直线
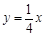相交于A、B两点．第一象限上的点M（m，n）（在A点左侧）是双曲线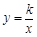上的动点．过点B作BD∥y轴交x轴于点D．过N（0，－n）作NC∥x轴交双曲线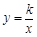于点E，交BD于点C．
（1）若点D坐标是（－8，0），求A、B两点坐标及k的值．
（2）若B是CD的中点，四边形OBCE的面积为4，求直线CM的解析式．
（3）设直线AM、BM分别与y轴相交于P、Q两点，且MA=pMP，MB=qMQ，求p－q的值．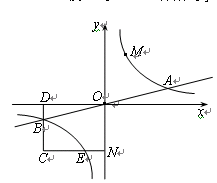
北京时间2011年3月11日13：46，在日本本州岛附近海域发生9.0级强震，中国政府迅速派出救援队前往救援。中国救援队发现在如图所示的展览厅内有一伤者等待救援．救援人员任选一个入口进入展览大厅，救助伤者后任选一个出口离开．
救援人员从进入到离开共有多少种可能的结果?(要求画出表格或树状图)
救援人员从入口A进入展厅并从北出口或西出口离开的概率是多少?
如图9，在8×8的正方形网格中，△ABC的顶点和线段EF的端点都在边长为1的小正方形的顶点上．
填空:∠ABC=___________，BC=___________；
请你在图中找出一点D，再连接DE、DF，使以D、E、F为顶点的三角形与△ABC全等．（画出一个三角形即可）
“五一”期间，某商场搞优惠促销，决定由顾客抽奖确定折扣．某顾客购买甲、乙两种商品，分别抽到七折（按售价的70％销售）和九折（按售价的90％销售），共付款386元，这两种商品原销售价之和为500元．问：这两种商品的原销售价分别为多少元？
如图，点B、E、C、F在一条直线上， BC＝EF，AB∥DE，∠A＝∠D．
ABC
DEF若AC＝3cm，求DF的长
解不等式组
解方程：
