已知向量m=(sin x,1),n= ,函数f(x)=(m+n)·m.
,函数f(x)=(m+n)·m.
(1)求函数f(x)的最小正周期T及单调递增区间;
(2)已知a,b,c分别为△ABC内角A,B,C的对边,A为锐角,a=2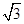 ,c=4,且f(A)是函数f(x)在
,c=4,且f(A)是函数f(x)在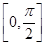 上的最大值,求△ABC的面积S.
上的最大值,求△ABC的面积S.
已知函数f(x)=x3-3ax2+3x+1.
(1)设a=2,求f(x)的单调区间;
(2)设f(x)在区间(2,3)中至少有一个极值点,求a的取值范围.
已知△ABC的内角A、B、C的对边分别为a、b、c,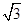 sin Ccos C-cos2C=
sin Ccos C-cos2C=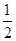 ,且c=3.
,且c=3.
(1)求角C;
(2)若向量m=(1,sin A)与n=(2,sin B)共线,求a、b的值.
设函数f(x)=ax2+(b-2)x+3(a≠0),若不等式f(x)>0的解集为(-1,3).
(1)求a,b的值;
(2)若函数f(x)在x∈[m,1]上的最小值为1,求实数m的值.
设函数f(x)=ex-ax-2.
(1)求f(x)的单调区间;
(2)若a=1,k为整数,且当x>0时,(x-k)f′(x)+x+1>0,求k的最大值.