自驾游从A地到B地有甲乙两条线路,甲线路是A-C-D-B,乙线路是A-E-F-G-H-B,其中CD段,EF段,GH段都是易堵车路段.假设这三条路段堵车与否相互独立.这三条路段的堵车概率及平均堵车时间如表所示.
| CD段 |
EF段 |
GH段 |
|
| 堵车概率 |
 |
 |
 |
| 平均堵车时间 (单位:小时) |
 |
2 |
1 |
经调查发现,堵车概率 在
在 上变化,
上变化, 在
在 上变化.
上变化.
在不堵车的情况下,走甲线路需汽油费500元,走乙线路需汽油费545元.而每堵车1小时,需多花汽油费20元.路政局为了估计 段平均堵车时间,调查了100名走甲线路的司机,得到下表数据.
段平均堵车时间,调查了100名走甲线路的司机,得到下表数据.
| 堵车时间(单位:小时) |
频数 |
| [0,1] |
8 |
| (1, 2] |
6 |
| (2, 3] |
38 |
| (3, 4] |
24 |
| (4, 5] |
24 |
(1)求 段平均堵车时间
段平均堵车时间 的值;
的值;
(2)若只考虑所花汽油费的期望值大小,为了节约,求选择走甲线路的概率.
已知圆 经过椭圆
经过椭圆 的右焦点
的右焦点 和上顶点
和上顶点 .
.
(1)求椭圆 的方程;
的方程;
(2)过原点 的射线
的射线 与椭圆
与椭圆 在第一象限的交点为
在第一象限的交点为 ,与圆
,与圆 的交点为
的交点为 ,
, 为
为 的中点,求
的中点,求 的最大值.
的最大值.
如图1,直角梯形 中,
中, ,
, ,
, ,点
,点 为线段
为线段 上异于
上异于 的点,且
的点,且 ,沿
,沿 将面
将面 折起,使平面
折起,使平面 平面
平面 ,如图2.
,如图2.
(1)求证: 平面
平面 ;
;
(2)当三棱锥 体积最大时,求平面
体积最大时,求平面 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
已知函数 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)若 是
是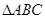 的三个内角,且
的三个内角,且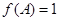 ,
,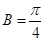 ,又
,又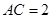 ,求
,求 边的长.
边的长.
已知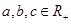 ,且
,且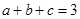 ,
, 的最小值为
的最小值为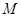 .
.
(1)求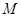 的值;
的值;
(2)解关于 的不等式
的不等式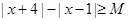 .
.