某城市现有人口总数为100万人,如果年自然增长率为1.2%,试解答下列问题:
⑴写出该城市人口数y(万人)与年份x(年)的函数关系式;
⑵用程序表示计算10年以后该城市人口总数的算法;
⑶用程序表示如下算法:计算大约多少年以后该城市人口将达到120万人.
如图,已知圆上的弧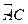 =
=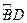 ,过C点的圆的切线与BA的延长线交
,过C点的圆的切线与BA的延长线交 于E点,证明:
于E点,证明:
证明:(Ⅰ)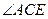 =
=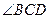 ;(Ⅱ)
;(Ⅱ) ;
;
(12分 )(12分)设a≥0,f(x)=x-1-ln2 x+2a ln x(x>0).
)(12分)设a≥0,f(x)=x-1-ln2 x+2a ln x(x>0).
(Ⅰ)令F(x)=xf'(x),讨论F (x)在(0,+∞)内的单调性并求极值;
(x)在(0,+∞)内的单调性并求极值;
(Ⅱ)求证:当x>1时,恒有x>ln2x -2a ln x+1
-2a ln x+1
轮船A和轮船B在中午12点整离开港口C,两艘轮船的航行方向之间的夹角为 ,轮船A的航行速度为25 千米/小时,轮船B的航行速度是15 千米/小时,下午2时两艘船的距离是多少?
,轮船A的航行速度为25 千米/小时,轮船B的航行速度是15 千米/小时,下午2时两艘船的距离是多少?
已知函数 (其中
(其中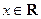 ),求:
),求:
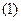 函数
函数 的最小正周期;
的最小正周期;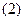 函数
函数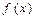 图象的对称轴和对称中心
图象的对称轴和对称中心
(12分) 在ΔABC中,已知 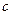 = 4,A = 45°,B = 15°,求a、b、和
= 4,A = 45°,B = 15°,求a、b、和