某检修小组乘汽车沿公路检修线路,约定前进为正,后退为负。某天自A地出发到收工时所走路线为(单位:千米):+10,-3,+4,+2,-8,+13,-2,+12,+8,+5.
(1)问收工时距A地有多远?
(2)若每千米路程耗油0.2升,问从A地出发到收工共耗油多少升?
八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
| 甲 |
7 |
8 |
9 |
7 |
10 |
10 |
9 |
10 |
10 |
10 |
| 乙 |
10 |
8 |
7 |
9 |
8 |
10 |
10 |
9 |
10 |
9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是_____分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4分2,则成绩较为整齐的是 队.
(1)先化简,再求值:(a+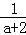 )÷(a﹣2+
)÷(a﹣2+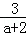 ),其中a=2
),其中a=2
(2)解分式方程: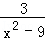 +
+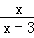 =1.
=1.
AB是⊙O的直径,AD与⊙O相交,点C是⊙O上一点,经过点C的直线交AD于点E.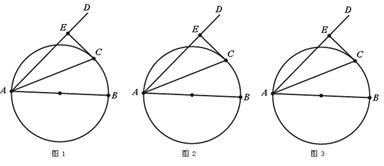
(1)如图1 ,若AC平分∠BAD,CE⊥AD于点E,求证:CE是⊙O的切线;
(2)如图2,若CE是⊙O的切线,CE⊥AD于点E,AC是∠BAD的平分线吗?说明理由;
(3)如图3,若CE是⊙O的切线,AC平分∠BAD,AB=8,AC=6,求AE的长度.
已知关于x的一元二次方程k -(4k+1)x+3k+3=0.
-(4k+1)x+3k+3=0.
(1)试说明:无论k取何值,方程总有两个实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5.当△ABC是等腰三角形时,求k的值.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4 ,求sinB的值.
,求sinB的值.