已知正方形的中心为直线x-y+1=0和2x+y+2=0的交点,正方形一边所在直线方程为x+3y-2=0,求其它三边方程。
已知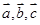 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 .
.
(1)若 ,且
,且 ,求:
,求: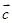 的坐标
的坐标
(2)若 ,且
,且 与
与 垂直,求
垂直,求 与
与 的夹角.
的夹角.
已知函数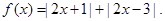
(1)求不等式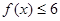 的解集;
的解集;
(2)若关于x的不等式 的解集非空,求实数
的解集非空,求实数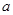 的取值范围.
的取值范围.
如图,已知四边形ABCD内接于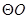 ,且AB是的
,且AB是的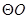 直径,过点D的
直径,过点D的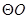 的切线与BA的延长线交于点M.
的切线与BA的延长线交于点M.
(1)若MD=6,MB=12,求AB的长;
(2)若AM=AD,求∠DCB的大小.
已知函数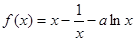
(1)若函数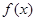 在点
在点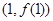 处的切线与圆
处的切线与圆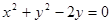 相切,求
相切,求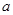 的值;
的值;
(2)当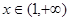 时,函数
时,函数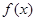 的图像恒在坐标轴
的图像恒在坐标轴 轴的上方,试求出
轴的上方,试求出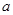 的取值范围.
的取值范围.
已知函数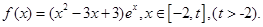
(1)当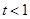 时,求函数
时,求函数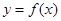 的单调区间;
的单调区间;
(2)当函数自变量的取值区间与对应函数值的取值区间相同时,这样的区间称为函数的保值区间. ,试问函数
,试问函数 在
在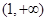 上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.
上是否存在保值区间?若存在,请求出一个保值区间;若不存在,请说明理由.