甲、乙等五名志愿者被随机地分到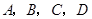 四个不同的岗位服务,每个岗位至少有一名志愿者.
四个不同的岗位服务,每个岗位至少有一名志愿者.
(Ⅰ)求甲、乙两人同时参加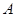 岗位服务的概率;
岗位服务的概率;
(Ⅱ)设随机变量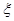 为这五名志愿者中参加
为这五名志愿者中参加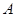 岗位服务的人数,求
岗位服务的人数,求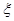 的分布列.
的分布列.
(共10分)已知等比数列 中,
中,
(Ⅰ)试求 的通项公式;
的通项公式;
(Ⅱ)若数列 满足:
满足: ,试求
,试求 的前
的前 项和公式
项和公式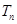
(共12分)已知函数 直线
直线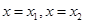 是
是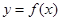 图像的任意两条对称轴,且
图像的任意两条对称轴,且 的最小值为
的最小值为 .
.
(1)求函数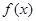 的单调增区间;
的单调增区间;
(2)求使不等式 的
的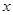 的取值范围.
的取值范围.
(3)若 求
求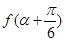 的值;
的值;
(共10分)
(1)解不等式: ;
;
(2)解关于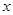 的不等式:
的不等式:
(本小题满分13分)如图,在平面直角坐标系 中,点
中,点 在单位圆
在单位圆 上,
上, ,且
,且 .
.
(1)若 ,求
,求 的值;
的值;
(2)若 也是单位圆
也是单位圆 上的点,且
上的点,且 .过点
.过点 分别做
分别做 轴的垂线,垂足为
轴的垂线,垂足为 ,记
,记 的面积为
的面积为 ,
, 的面积为
的面积为 .设
.设 ,求函数
,求函数 的最大值.
的最大值.
(本小题13分)已知函数 的一系列对应值如下表:
的一系列对应值如下表:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
(1)根据表格提供的数据求函数 的解析式;
的解析式;
(2)求函数 的单调递增区间和对称中心;
的单调递增区间和对称中心;
(3)若当 时,方程
时,方程 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围.
的取值范围.