(本小题13分)已知函数 的一系列对应值如下表:
的一系列对应值如下表:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
 |
|
 |
|
 |
(1)根据表格提供的数据求函数 的解析式;
的解析式;
(2)求函数 的单调递增区间和对称中心;
的单调递增区间和对称中心;
(3)若当 时,方程
时,方程 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围.
的取值范围.
现有6本不同的书,按下列要求各有多少种不同的分法:
(I)分为三份,每份2本;
(II)分给甲、乙、丙三人每人2本;
(III)分给甲、乙、丙三人;
(IV)分给甲、乙、丙三人,每人至少1本.
(最后结果请用数字表示).
设不在 轴下方的动点
轴下方的动点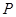 到
到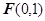 的距离比到
的距离比到 轴的距离大
轴的距离大
 求
求 的轨迹
的轨迹 的方程;
的方程; 过
过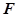 做一条直线
做一条直线 交轨迹
交轨迹 于
于 ,
, 两点,过
两点,过 ,
, 做切线交于
做切线交于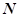 点,再过
点,再过 ,
, 做
做 的垂线,垂足为
的垂线,垂足为 ,若
,若 ,求此时点
,求此时点 的坐标.
的坐标.
已知函数 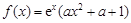
 R).
R).
(Ⅰ)若 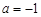 ,求曲线
,求曲线 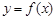 在点
在点  处的的切线方程;
处的的切线方程;
(Ⅱ)若  对任意
对任意 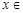
 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
已知函数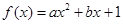 (
(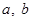 为实数,
为实数, ,
,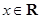 ).
).
(1) 当函数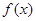 的图像过点
的图像过点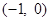 ,且方程
,且方程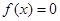 有且只有一个根,求
有且只有一个根,求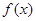 的表达式;
的表达式;
(2)若 当
当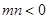 ,
, ,
, ,且函数
,且函数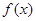 为偶函数
为偶函数
时,试判断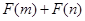 能否大于
能否大于 ?
?
设数列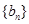 的前
的前 项和为
项和为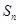 ,且
,且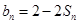 ;数列
;数列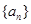 为等差数列,且
为等差数列,且 .
.
(1)求数列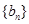 的通项公式;
的通项公式;
(2)若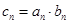 (
( ="1,2," 3…),
="1,2," 3…),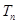 为数列
为数列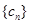 的前
的前 项和.求
项和.求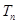 .
.