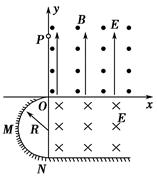
(14分)如下图，竖直平面坐标系
的第一象限，有垂直面向外的水平匀强磁场和竖直向上的匀强电场，大小分别为B和E；第四象限有垂直面向里的水平匀强电场,大小也为
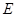；第三象限内有一绝缘光滑竖直放置的半径为
的半圆轨道,轨道最高点与坐标原点
相切,最低点与绝缘光滑水平面相切于
.一质量为
的带电小球从
轴上(
)的
点沿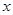
轴正方向进入第一象限后做圆周运动,恰好通过坐标原点,且水平切入半圆轨道并沿轨道内侧运动,过点水平进入第四象限,并在电场中运动(已知重力加速度为
).
(1)判断小球的带电性质并求出其所带电荷量；
(2)点距坐标原点至少多高；
(3)若该小球以满足(2)中
最小值的位置和对应速度进入第一象限,通过点开始计时,经时间
小球距坐标原点的距离
为多远？
据报道，一儿童玩耍时不慎从45m高的阳台上无初速度掉下，在他刚掉下时恰被楼下一社区管理人员发现，该人员迅速由静止冲向儿童下落处的正下方楼底，准备接住儿童.已知管理人员到楼底的距离为18m，为确保能稳妥安全接住儿童，管理人员将尽力节约时间，但又必须保证接住儿童时没有水平方向的冲击.不计空气阻力，将儿童和管理人员都看作质点，设管理人员奔跑过程中只做匀速或匀变速运动，g取10m/s2.
（1）管理人员至少用多大的平均速度跑到楼底？
（2）若管理人员在奔跑过程中做匀加速或匀减速运动的加速度大小相等，且最大速度不超过9m/s，求管理人员奔跑时加速度的大小需满足什么条件？
如图所示，ABC和DEF是在同一竖直平面内的两条光滑轨道，其中ABC的末端水平，DEF是半径为r=0.4m的半圆形轨道，其直径DF沿竖直方向，C、D可看作重合。现有一可视为质点的小球从轨道ABC上距C点高为H的地方由静止释放，
（1）若要使小球经C处水平进入轨道DEF且能沿轨道内侧运动，H至少要有多高？
（2）若小球静止释放处离C点的高度h小于（1）中H的最小值，小球可击中圆周上与圆心等高的E点，求h。（取g=10m/s2）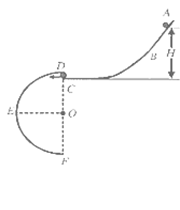
已知万有引力常量G，地球半径R，月球与地球间距离r，同步卫星距地面的高度h，月球绕地球的运转周期T1,地球自转周期T2,地球表面的重力加速度g ；某同学根据以上条件，提出一种估算地球质量M的方法：同步卫星绕地心做圆周运动，由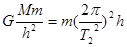
得
（1）请判断上面的结果是否正确，并说明理由。如不正确，请给出正确的解法和结果。
（2）请根据已知条件再提出两种估算地球质量的方法，并解得结果。
如图所示，小球沿光滑的水平面冲上一个光滑的半圆形轨道，已知轨道的半径为R，小球到达轨道的最高点时对轨道的压力大小恰好等于小球的重力。请求出：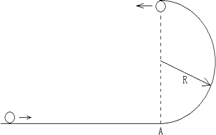
（1）小球到达轨道最高点时的速度为多大？
（2）小球落地时距离A点多远？落地时速度多大？
如图所示，光滑水平地面上有一足够长的木板，左端放置可视为质点的物体，其质量为m1=1kg,木板与物体间动摩擦因数u=0.1。二者以相同的初速度Vo="0.8m/s" —起向右运动，木板与竖直墙碰撞时间极短，且没有机械能损失。重力加速度g =10 m /s2。
I .如果木板质量m2=3kg,求物体相对木板滑动的最大距离；
II.如果木板质量m2=0.6kg,求物体相对木板滑动的最大距离。