如图,某船在上午11点30分在A处观测岛B在东偏北30o,该船以10海里/时的速度向东航行到C处,再观测海岛在东偏北60o,且船距海岛40海里.
(1)求船到达C点的时间;
(2)若该船从C点继续向东航行,何时到达B岛正南的D处?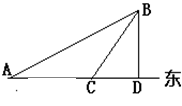
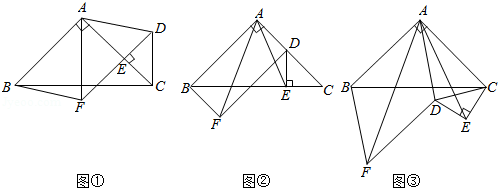
如图①,在 中, , ,点 在 上(且不与点 , 重合),在 的外部作 ,使 , ,连接 ,分别以 , 为邻边作平行四边形 ,连接 .
(1)请直接写出线段 , 的数量关系 ;
(2)将 绕点 逆时针旋转,当点 在线段 上时,如图②,连接 ,请判断线段 , 的数量关系,并证明你的结论;
(3)在图②的基础上,将 绕点 继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.
某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量 (本 与每本纪念册的售价 (元 之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)请直接写出 与 的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为 元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
如图,在 中, ,以 为直径的 分别交线段 , 于点 , ,过点 作 ,垂足为 ,线段 , 的延长线相交于点 .
(1)求证: 是 的切线;
(2)若 , ,求图中阴影部分的面积.
在一次课外实践活动中,同学们要测量某公园人工湖两侧 , 两个凉亭之间的距离.如图,现测得 , , 米,请计算 , 两个凉亭之间的距离(结果精确到1米)(参考数据: ,

在纪念中国抗日战争胜利70周年之际,某公司决定组织员工观看抗日战争题材的影片,门票有甲乙两种,甲种票比乙种票每张贵6元;买甲种票10张,乙种票15张共用去660元.
(1)求甲、乙两种门票每张各多少元?
(2)如果公司准备购买35张门票且购票费用不超过1000元,那么最多可购买多少张甲种票?