如右图所示，小球A和B带电荷量均为＋q，质量分别为m和2m，用不计质量的竖直细绳连接，在竖直向上的匀强电场中以速度v0匀速上升，某时刻细绳突然断开．小球A和B之间的相互作用力忽略不计．求：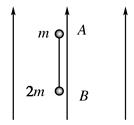
(1)该匀强电场的场强E.
(2)细绳断开后A、B两球的加速度aA、aB.
(10分)如图所示，一条轨道固定在竖直平面内，粗糙的ab段水平，bcde段光滑，cde段是以O为圆心、R为半径的一小段圆弧。可视为质点的物块A和B紧靠在一起，静止于b处
，A的质量是
B的3倍。两物块在足够大的内力作用下突然分离，分别向左、右始终沿轨道运动。B到d点时速度沿水平方向，此时轨道对B的支持力大小等于B所受重力的3/4，A与ab段的动摩擦因数为μ，重力加速度g，求：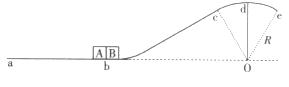
（1）物块B在d点的速度大小；
（2）物块A滑行的距离s。
(8分)空间探测器从某一星球表面竖直升空，已知探测器质量为500kg(设
为恒量)，发动机推力为恒力，探测器升空后发动机因故障而突然关闭，如图所示为探测器从升空到落回星球表面的速度-时间图象，则由图象可判断该探测器在星球表面所能达到的最大高度是多少？发动机工作时的推力又为多大？
17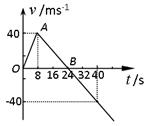
(6分)一辆汽车在平直的公路上做匀变速直线运动，该公路每隔60米就有一电线杆，汽车通过第一根和第二根电线杆用了5秒，通过第二根和第三根电线杆用了3秒。求：汽车的加速度和经过第一根电线杆时的瞬时速度。
如图所示的匀强电场中，有a、b、c三点，ab =2cm，bc =12cm，其中ab沿电场方向，bc和电场方向成60°角，一个电荷量为q＝4×10-8C的正电荷从a移到b电场力做功为W1＝1.2×10-7 J，求：
（1）匀强电场的场强E
（2）电荷从b移到c，电场力做功W2
一个电子以v0＝4×107m/s的速度，方向与电场方向相同，射入电场强度E＝2×105V/m的匀强电场中，如图。已知电子电量e＝－1.6×10－19C，电子质量m＝9.1×10-31，（忽略重力）.求：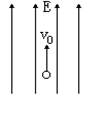
（1）从电子入射点到达速度为0的点的两点间电势差是多少？（2）电子到达速度为0的点所需的时间是多少？