小明所在学校初三学生综合素质评定分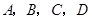 四个等第,为了了解评定情况,小明随机调查了初三30名学生的学号及他们的评定等第,结果整理如下:
四个等第,为了了解评定情况,小明随机调查了初三30名学生的学号及他们的评定等第,结果整理如下:
| 学号 |
3003 |
3008 |
3012 |
3016 |
3024 |
3028 |
3042 |
3048 |
3068 |
3075 |
| 等第 |
A |
C |
B |
C |
D |
B |
A |
B |
B |
A |
| 学号 |
3079 |
3088 |
3091 |
3104 |
3116 |
3118 |
3122 |
3136 |
3144 |
3154 |
| 等第 |
B |
B |
B |
C |
A |
C |
B |
A |
A |
B |
| 学号 |
3156 |
3163 |
3172 |
3188 |
3193 |
3199 |
3201 |
3208 |
3210 |
3229 |
| 等第 |
C |
A |
B |
B |
A |
B |
C |
C |
B |
B |
注:等第A,B,C,D分别代表优秀、良好、合格、不合格.
(1)请在下面给出的图中画出这30名学生综合素质评定等第的频数条形统计图,并计算其中等第达到良好以上(含良好)的频率.
(2)已知初三学生学号是从3001开始,按由小到大顺序排列的连续整数,请你计算这30名学生学号的中位数,并运用中位数的知识来估计这次初三学生评定等第达到良好以上(含良好)的人数.
如图,一艘渔船位于海洋观测站P的北偏东60°方向,渔船在A处与海洋观测站P的距离为60海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东45°方向上的B处。求此时渔船所在的B处与海洋观测站P的距离(结果保留根号)。
|

已知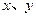 满足
满足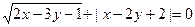 ,求
,求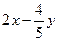 的平方根.
的平方根.
今年十月份,为方便民众出行,连江县成立了出租车公司,收费标准是:起步价5元,可乘坐3千米;3千米之后每千米加收1.8元.若某人乘坐了x千米,
(1)用代数式表示他应支付的费用;
(2)若他乘坐了13千米,应支付多少元?
为体现社会对老师的尊重,教师节这一天上午,出租车司机小王在东西向的公路上免费接送老师,如果规定向东为正,向西为负,出租车的行程如下(单位:千米) :+5,-4,+3,-10,+3,-9。
:+5,-4,+3,-10,+3,-9。
(1)最后一名老师送到目的时,小王距出租车出发点的距离是多少?
(2)若汽车耗油量为0.4升/千米,这天下午小王的汽车共耗油多少升?