如图，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点（P异于A、D），Q是BC边上的任意一点. 连AQ、DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于F.
（1）求证：△APE∽△ADQ；
（2）设AP的长为x，试求△PEF的面积S△PEF关于x的函数关系式，并求当P在何处时，S△PEF取得最大值？最大值为多少？
（3）当Q在何处时，△ADQ的周长最小？（须给出确定Q在何处的过程或方法，不必给出证明）
你能比较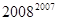
与
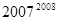的大小吗？
为了解决这个问题，我们首先写出它的一般形式，即比较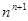
与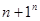
的大小（n是正整数），然后我们从分析n=1，n=2，n=3……中发现规律，经归纳、猜想得出结论
（1）通过计算，比较下列各组中两数的大小：（在横线上填写“＞”“＝”“＜”）
①1221，②2332；③3443；④4554；⑤5665
（2）从第（1）题的结果中，经过归纳，可以猜想出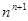与（n+1）n的大小关系是
（3）根据以上归纳．猜想得到的一般结论，试比较下列两数的大小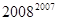：与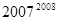
已知数轴上有A、B两点，A、B间的距离是2，点A与原点距离是3．
（1）B点表示的数是什么？
（2）B点表示的这些数的和是多少？
（3）所有满足条件的B点与原点的距离之和是多少？
一跳蚤在一直线上从O点开始，第1次向右跳1个单位，紧接着第2次向左跳2个单位，第3次向右跳3个单位，第4次向左跳4个单位，……，依此规律跳下去，当它跳第100次落下时，落点处离O点的距离是多少个单位？写出你的计算过程。
若│a│=2，│b│=5且│a+b│=a+b，求a—b的值
计算：-4.037
12+7.53712-36（
）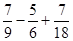