在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5 月1日至30日,评委会把同学们上交作品的件数按5天一组分组统计,绘制了频率分布直方图(如图),已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请回答下列问题: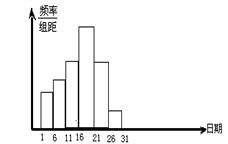
(1)本次活动共有多少件作品参加评比?
(2)经过评比,第四组和第六组分别有10件和2件 作品获奖,问这两组哪组获奖率更高?
(本小题满分为12分)椭圆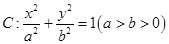 的左、右焦点分别为
的左、右焦点分别为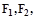 上顶点为
上顶点为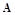 ,在
,在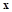 轴负半轴上有一点
轴负半轴上有一点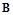 ,满足
,满足
(Ⅰ)求椭圆 的离心率.
的离心率.
(Ⅱ)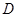 是过
是过 三点的圆上的点,
三点的圆上的点,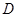 到直线
到直线 的最大距离等于椭圆长轴的长,求椭圆
的最大距离等于椭圆长轴的长,求椭圆 的方程.
的方程.
(本小题满分为12分)某校从高一年级学生中随机抽取40名学生作为样本,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六组: ,
, ,,
,, 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.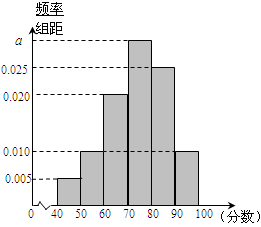
(Ⅰ)求图中实数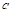 的值;
的值;
(Ⅱ)若该校高一年级共有学生500人,试估计该校高一年级在考试中成绩不低于60分的人数;
(Ⅲ)若从样本中数学成绩在 与
与 两个分数段内的学生中随机选取两名学生,试用列举法求这两名学生的数学成绩之差的绝对值不大于10的概率.
两个分数段内的学生中随机选取两名学生,试用列举法求这两名学生的数学成绩之差的绝对值不大于10的概率.
(本小题满分为12分)已知四棱锥P—ABCD及其三视图如下图所示,E是侧棱PC上的动点。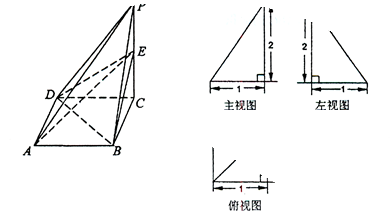
(Ⅰ)求四棱锥P—ABCD的体积;
(Ⅱ)不论点E在何位置,是否都有BD AE?试证明你的结论;
AE?试证明你的结论;
(Ⅲ)若点E为PC的中点,求二面角D—AE—B的大小。
(本小题满分为10分)在数列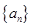 中,
中,
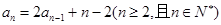
(Ⅰ)求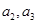 的值;
的值;
(Ⅱ)证明:数列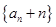 是等比数列,并求
是等比数列,并求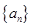 的通项公式
的通项公式
(本小题满分10分)选修4-5:不等式选讲
已知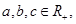 且
且 .证明:
.证明:
(Ⅰ)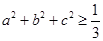 ;
;
(Ⅱ) .
.