某车站在春运期间为了了解旅客购票情况，随机抽样调查了100名旅客从开始在售票窗口排队到购到车票所用的时间t(以下简称为购票用时，单位为min)，下面是这次调查统计分析得到的频率分布表和频率分布直方图(如图所示).
| 分组 |
频数 |
频率 |
|
| 一组 |
0≤t<5 |
0 |
0 |
| 二组 |
5≤t<10 |
10 |
0.10 |
| 三组 |
10≤t<15 |
10 |
② |
| 四组 |
15≤t<20 |
① |
0.50 |
| 五组 |
20≤t≤25 |
30 |
0.30 |
| 合计 |
100 |
1.00 |
|
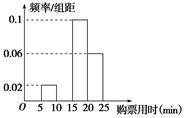
解答下列问题：
(1)这次抽样的样本容量是多少？
(2)在表中填写出缺失的数据并补全频率分布直方图；
(3)旅客购票用时的平均数可能落在哪一组？
（ 14分 ）已知圆C：x2+y2-2x+4y-4=0,是否存在斜率为1的直线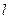
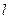,使以被圆C所截得的弦AB为直径的圆经过原点？若存在,写出直线的方程；若不存在,请说明理由.
（ 12分 ）如图,已知三棱锥A-BPC中,AP⊥PC,AC⊥BC,M为AB中点,D为PB中点,且△PMB为正三角形. 
(1)求证:DM∥平面APC;
(2)求证:平面ABC⊥平面APC;
(3)若BC=4,AB=20,求三棱锥D-BCM的体积.
（ 12分 ）已知汽车从刹车到停车所滑行的距离s(m)与速度v( m/s)的平方及汽车的总重量t(t)的乘积成正比.设某辆卡车不装货物以50 m/s行驶时，从刹车到停车滑行了20 m.如果这辆车装载着与车身相等重量的货物行驶，并与前面的车辆距离为15 m(假设卡车司机从发现前面车辆停车到自己刹车需耽搁1 s)，为了保证前面车辆紧急停车时不与后面车辆撞车，最大限制速度是多少?
设关于
的函数
的最大值为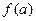
（1）求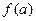的表达式
（2）确定使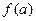=5的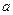
的值，并对此时的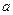，求
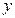的最小值
已知函数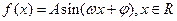
（其中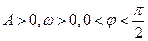
）的图象与x轴的交点中，相邻两个交点之间的距离为
，且图象上一个最低点为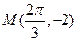
.
(1)求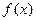
的解析式；
（2）用五点作图法做出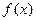的图像
（3）说明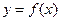
的图象是由
的图象经过怎样的变换得到
（4）求函数的单调递减区间
（5）当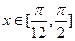
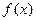，求的值域.