如图,在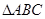 中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DC,连接CF。
中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交BE的延长线于F,且AF=DC,连接CF。
(1)求证:D是BC的中点;
(2)如果AB=AC,试猜测四边形ADCF的形状,并证明你的结论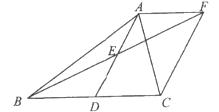
如图,在⊙O 中,直径AB交弦ED于点G,EG=DG,⊙O的切线BC交DO的延长线于点C,F是DC与⊙O的交点,连结AF.
(1)求证:DE∥BC;
(2)若OD=1,CF=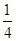 ,求AF的长.
,求AF的长.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).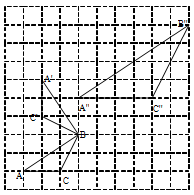
(1)将△ABC绕点B顺时针旋转90°得到△A’BC ’,请画出△A’BC ’,并求BA边旋转到B A’’位置时所扫过图形的面积;
(2)请在网格中画出一个格点△A”B”C”,使△A”B”C”∽△ABC,且相似比不为1.
在一个不透明的箱子里,装有黄、白、黑各一个球,它们除了颜色之外没有其他区别.
(1)随机从箱子里取出1个球,则取出黄球的概率是多少?
(2)随机从箱子里取出1个球,放回搅匀再取第二个球,请你用画树状图或列表的方法表示出所有可能出现的结果,并求两次取出的都是白色球的概率.
如图,在四边形ABCD中,∠A=30°,∠C=90°,∠ADB=105°,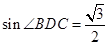 ,AD=4.
,AD=4.
求DC的长.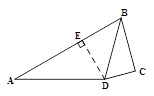
已知:抛物线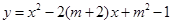 与x轴有两个交点.
与x轴有两个交点.
(1)求m的取值范围;
(2)当m为非正整数时,关于x的一元二次方程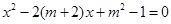 有整数根,求m的值.
有整数根,求m的值.