化简:
已知抛物线 经过点(3,0),(-1,0).
经过点(3,0),(-1,0).
(1)求抛物线的解析式;
(2)求抛物线的顶点坐标.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB•AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 的值.
的值.
如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾斜度由45°降为30°,已知原滑滑板的长为5米,点、、在同一水平地面上.
求:改善后滑滑板会加长多少?(精确到0.01)(参考数据: =1.414,
=1.414, =1.732,
=1.732, =2.449)
=2.449)
如图,在平面直角坐标系中,已知点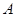 坐标为(2,4),直线x=2与
坐标为(2,4),直线x=2与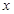 轴相交于点
轴相交于点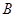 ,连结
,连结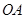 ,抛物线y=x
,抛物线y=x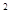
 从点
从点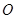 沿
沿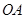 方向平移,与直线x=2交于点
方向平移,与直线x=2交于点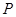 ,顶点
,顶点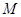 到
到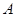 点时停止移动.
点时停止移动.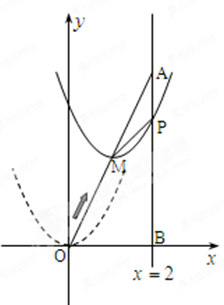
(1)求线段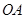 所在直线的函数解析式;
所在直线的函数解析式;
(2)设抛物线顶点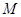 的横坐标为
的横坐标为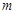 ,
,
①用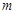 的代数式表示点
的代数式表示点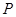 的坐标;
的坐标;
②当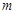 为何值时,线段
为何值时,线段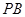 最短;
最短;
(3)当线段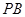 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点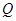 ,使△
,使△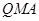 的面积与△
的面积与△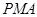 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点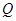 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
某跳水运动员进行10m跳台跳水的训练时,身体(看成一点)在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为己知条件).在跳某个规定动作时,正确情况下,该运动员在空中的最高处距水面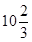 m,入水处与池边的距离为4m, 同时,运动员在距水面高度为5m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
m,入水处与池边的距离为4m, 同时,运动员在距水面高度为5m以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.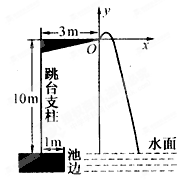
(l)求这条抛物线的解析式;
(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为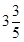 ,问:此次跳水会不会失误?通过计算说明理由.
,问:此次跳水会不会失误?通过计算说明理由.