如图,在平面直角坐标系中,已知点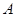 坐标为(2,4),直线x=2与
坐标为(2,4),直线x=2与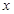 轴相交于点
轴相交于点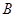 ,连结
,连结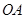 ,抛物线y=x
,抛物线y=x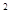
 从点
从点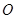 沿
沿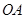 方向平移,与直线x=2交于点
方向平移,与直线x=2交于点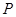 ,顶点
,顶点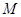 到
到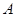 点时停止移动.
点时停止移动.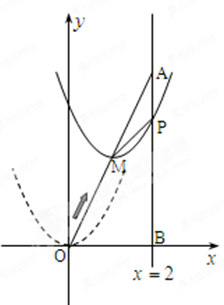
(1)求线段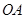 所在直线的函数解析式;
所在直线的函数解析式;
(2)设抛物线顶点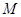 的横坐标为
的横坐标为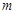 ,
,
①用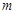 的代数式表示点
的代数式表示点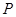 的坐标;
的坐标;
②当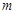 为何值时,线段
为何值时,线段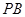 最短;
最短;
(3)当线段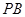 最短时,相应的抛物线上是否存在点
最短时,相应的抛物线上是否存在点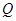 ,使△
,使△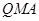 的面积与△
的面积与△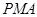 的面积相等,若存在,请求出点
的面积相等,若存在,请求出点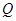 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
甲、乙、丙三人进行羽毛球比赛,他们通过摸球的方式决定首场比赛的两个选手:在一个不透明的口袋中放入两个红球和一个白球,它们除颜色外其他都相同,将它们搅匀,三人从中各摸出一个球,摸到红球的两人即为首场比赛选手.求甲、乙两人成为比赛选手的概率.(请用画树状图或列表等方法写出分析过程并给出结果)
某数学课外学习小组为统计某小区共享单车的使用情况,对 、 、 、 四种共享单车品牌的骑行人数进行了调查,并绘制了如下的两张不完整的统计图.
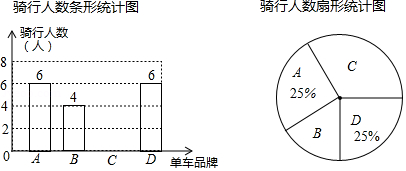
(1)扇形统计图中, 、 品牌单车骑行人数所占圆心角的度数分别为 和 ;
(2)请把条形统计图补充完整;
(3)若该小区习惯使用共享单车的有120人,请你估算使用 型品牌单车的人数约是多少人?
在学校组织的朗诵比赛中,甲、乙两名学生以抽签的方式从3篇不同的文章中抽取一篇参加比赛,抽签规则是:在3个相同的标签上分别标注字母 、 、 ,各代表1篇文章,一名学生随机抽取一个标签后放回,另一名学生再随机抽取.用画树状图或列表的方法列出所有等可能的结果,并求甲、乙抽中同一篇文章的概率.
桌面上有四张正面分别标有数字1,2,3,4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗匀.
(1)随机翻开一张卡片,正面所标数字大于2的概率为 ;
(2)随机翻开一张卡片,从余下的三张卡片中再翻开一张,求翻开的两张卡片正面所标数字之和是偶数的概率.
某校为了解八年级学生最喜欢的球类情况,随机抽取了八年级部分学生进行问卷调查,调查分为最喜欢篮球、乒乓球、足球、排球共四种情况,每名同学选且只选一项,现将调查结果绘制成如下所示的两幅统计图.
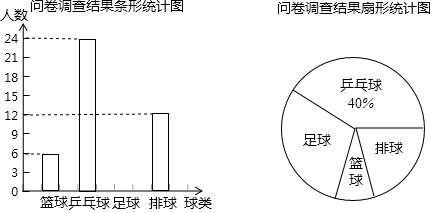
请结合这两幅统计图,解决下列问题:
(1)在这次问卷调查中,一共抽取了 名学生;
(2)请补全条形统计图;
(3)若该校八年级共有300名学生,请你估计其中最喜欢排球的学生人数.