阅读材料:黑白双雄,纵横江湖;双剑合壁,天下无敌.这是武侠小说中的常见描述,其意指两个人合在一起,取长补短,威力无比.在二次根式中也有这样相辅相成的例子.
如 ,
,
它们的积是有理数,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.于是,二次根式除法可以这样解:
如 ,
,
象这样,通过分子、分母同乘以一个式子把分母中的根号化去或根号中的分母化去,叫做分母有理化.
解决问题:
(1) 的有理化因式是 .
的有理化因式是 .  分母有理化得 .
分母有理化得 .
(2)分母有理化:(1)  ="_________;(2)"
="_________;(2)"  ="________;(3)"
="________;(3)"  =______..
=______..
(3)计算:  .
.
分解因式: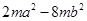
已知:如图,在△ABC中,AB=AC,∠BAC=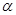 ,且60°<
,且60°<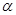 <120°.P为△ABC内部一点,且PC=AC,∠PCA=120°—
<120°.P为△ABC内部一点,且PC=AC,∠PCA=120°—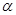 .
.
(1)用含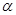 的代数式表示∠APC,得∠APC =_______________________;
的代数式表示∠APC,得∠APC =_______________________;
(2)求证:∠BAP=∠PCB;
(3)求∠PBC的度数.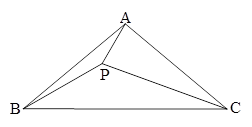
观察例题:
∵ ,即
,即 ,
,
∴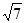 的整数部分为2,小数部分为
的整数部分为2,小数部分为 。
。
请你观察上述的规律后试解下面的问题: 如果 的小数部分为
的小数部分为 ,
, 的小数部分为
的小数部分为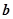 ,求
,求 的值.
的值.
如图⑴,一等腰直角三角尺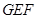 (
( )的两条直角边与正方形
)的两条直角边与正方形 的两条边分别重合在一起. 现正方形
的两条边分别重合在一起. 现正方形 保持不动,将三角尺
保持不动,将三角尺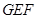 绕斜边
绕斜边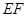 的中点
的中点 (点
(点 也是
也是 中点)旋转.
中点)旋转.
①若将三角尺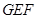 绕斜边
绕斜边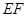 的中点
的中点 按顺时针方向旋转到如图⑵,当
按顺时针方向旋转到如图⑵,当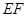 与
与 相交于点
相交于点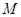 ,
,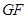 与
与 相交于点
相交于点 时,通过观察或测量
时,通过观察或测量 、
、 的长度,猜想
的长度,猜想 、
、 满足的数量关系,并证明你的猜想;
满足的数量关系,并证明你的猜想;
②若三角尺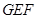 旋转到如图⑶所示的位置时,线段
旋转到如图⑶所示的位置时,线段 的延长线与
的延长线与 的延长线相交于点
的延长线相交于点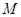 ,线
,线 的延长线与
的延长线与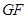 的延长线相交于点
的延长线相交于点 ,此时,①中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
,此时,①中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
如图,△ABC是等边三角形,D是BC边的中点,点 E在AC的延长线上,且∠CDE=30°.若AD= ,求DE的长.
,求DE的长.