如图，半径为1个单位的圆片上有一点Q与数轴上的原点重合（提示:圆的周长C=2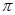
r）
（1） 把圆片沿数轴向左滚动1周，点Q到达数轴上点A的位置，点A表示的数是_________；
（2）圆片在数轴上向右滚动的周数记为正数，圆片在数轴上向左滚动的周数记为负数，依次运动情况记录
如下：+2, -1, -5, +4, +3, -2
①第几次滚动后,Q点距离原点最近？第几次滚动后,Q点距离原点最远？
②当圆片结束运动时，Q点运动的路程共有多少?此时点Q所表示的数是多少?
如图，A，P，B，C是半径为8的⊙O上的四点，且满足∠BAC=∠APC=60°，
（1）求证：△ABC是等边三角形；
（2）求圆心O到BC的距离OD．
某班数学科代表小华对本班上期期末考试数学成绩作了统计分析，绘制成如下频数、频率统计表和频数分布直方图，请你根据图表提供的信息，解答下列问题：
| 分组 |
49.5～59.5 |
59.5～69.5 |
69.5～79.5 |
79.5～89.5 |
89.5～100.5 |
合计 |
| 频数 |
2 |
a |
20 |
16 |
4 |
50 |
| 频率 |
0.04 |
0.16 |
0.40 |
0.32 |
b |
1 |
（1）频数、频率统计表中，a= ；b= ；
（2）请将频数分布直方图补充完整；
（3）小华在班上任选一名同学，该同学成绩不低于80分的概率是多少？
先化简，再求值：
-，其中a=﹣2，b=1．
如图，抛物线
与x轴交于A、B两点，与y轴交于点C，连接BC、AC．
（1）求AB和OC的长；
（2）点E从点A出发，沿x轴向点B运动（点E与点A、B不重合），过点E作直线l平行BC，交AC于点D．设AE的长为m，△ADE的面积为s，求s关于m的函数关系式，并写出自变量m的取值范围；
（3）在（2）的条件下，连接CE，求△CDE面积的最大值；此时，求出以点E为圆心，与BC相切的圆的面积（结果保留π）．
如图，在矩形纸片ABCD中，AB=6，BC=8．把△BCD沿对角线BD折叠，使点C落在C′处，BC′交AD于点G；E、F分别是C′D和BD上的点，线段EF交AD于点H，把△FDE沿EF折叠，使点D落在D′处，点D′恰好与点A重合．
（1）求证：△ABG≌△C′DG；
（2）求tan∠ABG的值；
（3）求EF的长．