如图，梯形ABCD中，BC∥AD,∠ABC=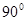
,对角线AC与BD相交于O,AB=8cm,AD=10cm,BC=6cm,一个动点E从点B出发，以每秒1cm的速度沿射线BA方向移动，过E作EQ⊥AB,交直线AC于P,交直线BD于Q，以PQ为边向上作正方形PQMN,设正方形PQMN与△BOC,重叠部分的面积为s，点E的运动时间为t秒.
（1）求PQ经过O 点时的运动时间t；
（2）求s与t的函数关系式，并求s的最大值;
（3）如图（2），若AB的中点为H，DK=1,过H作HT∥AD,交BD于T,交BK于G,求G在正方形PQMN内部时t的取值范围。
如图，在⊙O中，CD为直径，AB为弦，且CD平分AB于E，OE=3cm，AB=8cm求：⊙O的半径．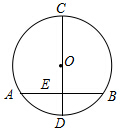
解方程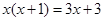
解方程：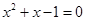
．
如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），与y轴交于C（0，﹣3）点，点P是直线BC下方的抛物线上一动点．
（1）求这个二次函数的表达式．
（2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．
（3）当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的最大面积．
小明家所在居民楼的对面有一座大厦AB，AB=
米．为测量这座居民楼与大厦之间的距离，小明从自己家的窗户C处测得大厦顶部A的仰角为37°，大厦底部B的俯角为48°．求小明家所在居民楼与大厦的距离CD的长度．（结果保留整数）（参考数据：
）