已知万有引力常量G,地球半径R,月球和地球之间的距离r,同步卫星距地面的高度h,月球绕地球的运转周期T1,地球的自转周期T2,地球表面的重力加速度g。某同学根据以上条件,提出一种估算地球质量M的方法:
同步卫星绕地球作圆周运动,由 得
得
⑴请判断上面的结果是否正确,并说明理由。如不正确,请给出正确的解法和结果。
⑵请根据已知条件再提出两种估算地球质量的方法并解得结果。
已知某行星半径为 ,以其第一宇宙速度运行的卫星的绕行周期为
,以其第一宇宙速度运行的卫星的绕行周期为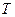 ,该行星上发射的同步卫星的运行速度为
,该行星上发射的同步卫星的运行速度为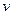 .求
.求
(1)同步卫星距行星表面的高度为多少?
(2)该行星的自转周期为多少?
如图所示,长L=75cm的质量m=2kg的平底玻璃管底部置有一玻璃小球,玻璃管从静止开始受到一竖直向下的恒力F=12N的作用,使玻璃管竖直向下运动,经一段时间t,小球离开管口.空气阻力不计,取g=10m/s2.求:时间t和小球离开玻璃管时玻璃管的速度的大小.
一列货车以28.8km/h的速度在铁路上运行,由于调度事故,在货车后面700m处有一列快车以72km/h的速度在行驶,快车司机发觉后立即合上制动器,但快车要滑行2000m才能停下来,则:
(1)试判断两车会不会相撞,并说明理由。
(2)若不相撞,求两车相距最近时的距离。若相撞,求快车刹车后经多长时间与货车相撞?
一物体放到水平地板上,用一轻弹簧水平拉该物体,当物体刚开始运动时,弹簧伸长了3cm,当拉着物体匀速前进时,弹簧伸长了2cm,用弹簧测量此物体的重力时,弹簧伸长了10cm,己知弹簧的劲度系数为k=200N/m,求:
(1)物体所受的最大静摩擦力;
(2)物体和地板间的动摩擦因数。
如图所示,在2009年10月1日国庆阅兵演习中,某直升飞机在地面上空某高度A位置处于静止状态待命,接上级命令,要求该机10时58分由静止状态沿水平方向做匀加速直线运动,10时58分50秒到达B位置,然后就进入BC段的匀速受阅区,10时59分40秒准时通过C位置,已知SBC=10km。问:
(1)直升飞机在BC段的速度大小是多少?
(2)直升飞机在AB段做匀加速直线运动时的加速度大小是多少?
(3)AB段的距离为多少?