如图,AB是⊙O的直径,CD切⊙O于点C,BE⊥CD于E,连接AC、BC.
(1)求证:BC平分∠ABE;
(2)若⊙O的半径为2,∠A =60°,求CE的长.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0)、B(3,0)两点,直线L与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求抛物线的解析式及直线AC的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
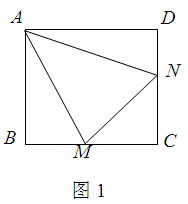
已知:正方形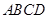 中,
中,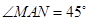 ,
,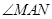 绕点
绕点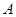 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交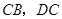 (或它们的延长线)于点
(或它们的延长线)于点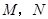 .当
.当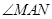 绕点
绕点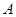 旋转到
旋转到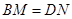 时(如图1),易证
时(如图1),易证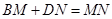 .
.
(1)当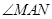 绕点
绕点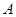 旋转到
旋转到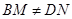 时(如图2),线段
时(如图2),线段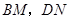 和
和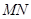 之间有怎样的数量关系?写出猜想,并加以证明.
之间有怎样的数量关系?写出猜想,并加以证明.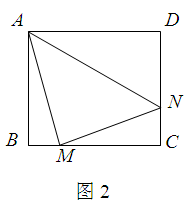
(2)当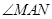 绕点
绕点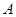 旋转到如图3的位置时,线段
旋转到如图3的位置时,线段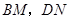 和
和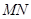 之间又有怎样的数量关系?请直接写出你的猜想.
之间又有怎样的数量关系?请直接写出你的猜想.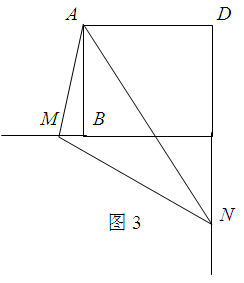
当今社会手机越来越普及,有很多人开始过份依赖手机,一天中使用手机时间过长而形成了“手机瘾”.为了解我校初三年级学生的手机使用情况,学生会随机调查了部分学生的手机使用时间,将调查结果分成五类:A.基本不用;B,平均一天使用1—2小时;C.平均一天使用2—4小时;D.平均一天使用4—6小时:E.平均一天使用超过6小时.并用得到的数据绘制成了如下两幅不完整的统计图,请根据相关信息,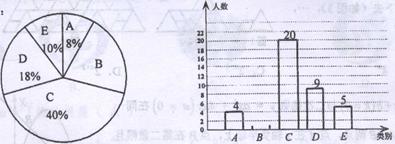
解答下列问题
(1)将上面的条形统计图补充完整;
(2)若一天中手机使用时间趣过6小时,则患有严重的“手机瘾”.我校初三年级共有1490人,试估计我校初三年级中约有多少人患有严重的“手机瘾”:
(3)在被调查的基本不用手机的4位同学中有2男2女,现要从中随机再抽两名同学去参加座谈,请你用列表法或树状图方法求出所选两位同学恰好是一名男同学和一位女同学的概率.
某镇道路改造工程,由甲、乙两工程队合作20天可完成.甲工程队单独施工比乙工程队单独施工多用30天完成此项工程.
(1)求甲、乙两工程队单独完成此项工程各需要多少天?
(2)若甲工程队独做a天后,再由甲、乙两工程队合作天(用含a的代数式表示)可完成此项工程;
(3)如果甲工程队施工每天需付施工费1万元,乙工程队施工每天需付施工费2.5万元,甲工程队至少要单独施工多少天后,再由甲、乙两工程队合作施工完成剩下的工程,才能使施工费不超过64万元?
化简求值: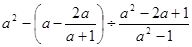 ,其中
,其中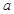 是方程
是方程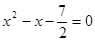 的解
的解