如图10,在平面直角坐标系中,正方形OABC边长是4,点A、C分别在y轴、x轴的正半轴上.动点P从点A开始,以每秒2个单位长度的速度在线段AB上来回运动.动点Q从点B开始沿B→C→O的方向,以每秒1个单位长度的速度向点O运动.P、Q两点同时出发,当点Q到达点O时,P、Q两点同时停止运动.设运动时间为t,△OPQ的面积为S.
(1)当t =1时,S = ;
(2)当0≤ t ≤ 2时,求满足△BPQ的面积有最大值的P、Q两点坐标;
(3)在P、Q两点运动的过程中,是否存在某一时刻,使得S = 6.若存在,请直接写出所有符合条件的P点坐标;若不存在,请说明理由.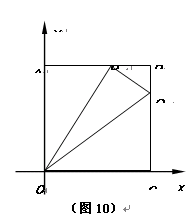
目前世界上最高的电视塔是广州新电视塔.如图8所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.
(1)求大楼与电视塔之间的距离AC;
(2)求大楼的高度CD(精确到1米)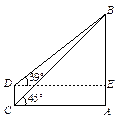
如图,从参加环保知识竞赛的 学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下:
学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下: 观察图形,回答下列问题:
观察图形,回答下列问题:
(1)79.5---89.5这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率(60分及以上为及格)
已知一个样本,27,23,25,27,29,31,27,30,32,31,28,26,27,29,28,24,26,27,28,30,以2为组距画出频数分布直方图
2 011年某车站在春运期间为改进服务,抽查了100名旅客从开始在窗口排队到购到车票所用时间t(以下简称购票时间,单位:分),得到如下表所示的频数分布表。
011年某车站在春运期间为改进服务,抽查了100名旅客从开始在窗口排队到购到车票所用时间t(以下简称购票时间,单位:分),得到如下表所示的频数分布表。
| 分组 |
频数 |
频率 |
|
| 一组 |
0 <5 <5 |
0 |
0 |
| 二组 |
5 <10 <10 |
10 |
0.10 |
| 三组 |
10 <15 <15 |
10 |
|
| 四组 |
15 <20 <20 |
0.50 |
|
| 五组 |
20 <25 <25 |
30 |
0.30 |
| 合计 |
100 |
1.00 |
(1)在表中填写缺失的数据;
(2)画出频数分布直方图;
(3)求购票时间的平均数
(4)若每增加一个购票窗口可以使平均购票用时降低5分,要使平均购票用时不超过10分,那么 决策一下至少要增加几个窗口?
七年级(1)班40个学生某次数学测验成绩如下(单位:分):
63 84 91 53 69 81 61 69 91 78
75 81 80 67 76 81 79 94 61  69
69
89 70 70 87 81 86 90 88 85 67
67
71 82 87 75 87 95 53 65 74 77
数学老师按10分的组距分段,算出每个分数段学生成绩出现的频数,填入频数分布表.
(1)请把频数分布表及频数分布直方图补充完整;
(2)请你帮老师统计一下这次数学考试的及格率(60分以上含60分为及格)及优秀率(90分以上含90分为优秀);
(3)请说明哪个分数段的学生最多?哪个分数段的学生最少?
(4)绘制频数折线图.