一个工厂在某年里每月产品的总成本y(万元)与该月产量x(万件)之间有如下组对应数据:
| x |
1.08 |
1.12 |
1.19 |
1.28 |
1.36 |
1.48 |
1.59 |
1.68 |
1.80 |
1.87 |
1.98 |
2.07 |
| y |
2.25 |
2.37 |
2.40 |
2.55 |
2.64 |
2.75 |
2.92 |
3.03 |
3.14 |
3.26 |
3.36 |
3.50 |
(1)画出散点图;
(2)求月总成本y与月总产量x之间的回归直线方程.
为了更好地开展社团活动,丰富同学们的课余生活,现用分层抽样的方法从“模拟联合国”,“街舞”,“动漫”,“话剧”四个社团中抽取若干人组成校社团指导小组,有关数据见下表:(单位:人)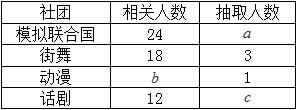
(Ⅰ)求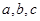 的值;
的值;
(Ⅱ)若从“模拟联合国”与“话剧”社团已抽取的人中选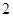 人担任指导小组组长,求这
人担任指导小组组长,求这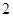 人分别来自这两个社团的概率.
人分别来自这两个社团的概率.
已知函数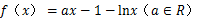
(1)讨论函数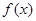 的单调性;
的单调性;
(2)若函数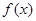 在
在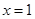 处取得极值,不等式
处取得极值,不等式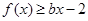 对
对 恒成立,求实数
恒成立,求实数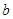 的取值范围;
的取值范围;
(3)当 时,证明不等式.
时,证明不等式.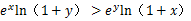
已知平面内一动点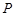 到点
到点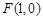 的距离等于它到直线
的距离等于它到直线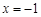 的距离.
的距离.
(Ⅰ)求动点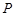 的轨迹
的轨迹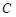 的方程;
的方程;
(Ⅱ)若直线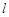 与曲线
与曲线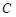 交于
交于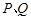 两点,且
两点,且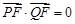 ,又点
,又点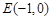 ,求
,求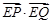 的最小值.
的最小值.
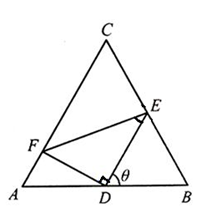
如图,正三角形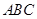 的边长为
的边长为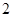 ,D,E,F分别在三边AB,BC和CA上,且D为AB的中点,
,D,E,F分别在三边AB,BC和CA上,且D为AB的中点,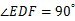 ,
,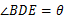 ,
,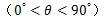 .
.
(1)当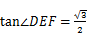 时,求
时,求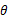 的大小;
的大小;
(2)求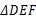 的面积S的最小值及使S得取最小值时的
的面积S的最小值及使S得取最小值时的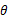 值.
值.
如图,在三棱柱  中,已知
中,已知 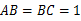 ,
, ,
, 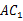 与平面
与平面 所成角为
所成角为 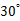 ,
,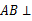 平面
平面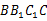 .
.
(Ⅰ)求证: ; (Ⅱ)求三棱锥
; (Ⅱ)求三棱锥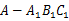 的高.
的高.