为了更好地开展社团活动,丰富同学们的课余生活,现用分层抽样的方法从“模拟联合国”,“街舞”,“动漫”,“话剧”四个社团中抽取若干人组成校社团指导小组,有关数据见下表:(单位:人)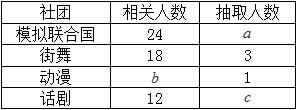
(Ⅰ)求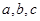 的值;
的值;
(Ⅱ)若从“模拟联合国”与“话剧”社团已抽取的人中选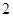 人担任指导小组组长,求这
人担任指导小组组长,求这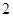 人分别来自这两个社团的概率.
人分别来自这两个社团的概率.
(本小题满分12分)设各项均为正数的数列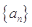 的前
的前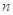 项和为
项和为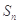 ,满足
,满足
 且
且 构成等比数列.
构成等比数列.
(Ⅰ)求数列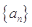 的通项公式;
的通项公式;
(Ⅱ)证明:对一切正整数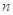 ,有
,有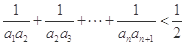 .
.
(本小题满分14分)设函数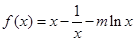 .
.
(Ⅰ)若函数 在定义域上为增函数,求实数
在定义域上为增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)在(Ⅰ)的条件下,若函数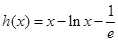 ,
, 使得
使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分13分)如图,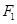 、
、 为椭圆
为椭圆 的左、右焦点,
的左、右焦点,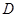 、
、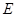 是椭圆的两个顶点,椭圆的离心率
是椭圆的两个顶点,椭圆的离心率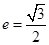 ,
, .若
.若 在椭圆
在椭圆 上,则点
上,则点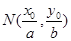 称为点
称为点 的一个“好点”.直线
的一个“好点”.直线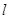 与椭圆交于
与椭圆交于 、
、 两点,
两点,  、
、 两点的“好点”分别为
两点的“好点”分别为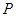 、
、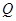 ,已知以
,已知以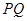 为直径的圆经过坐标原点.
为直径的圆经过坐标原点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)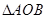 的面积是否为定值?若为定值,试求出该定值;若不为定值,请说明理由.
的面积是否为定值?若为定值,试求出该定值;若不为定值,请说明理由.
(本小题满分14分)椭圆 ,椭圆的左、右焦点分别为
,椭圆的左、右焦点分别为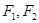 ,椭圆上的点到中心的最短距离为
,椭圆上的点到中心的最短距离为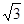 ,且椭圆上的点到左焦点
,且椭圆上的点到左焦点 的最长距离为
的最长距离为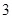 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若直线 交
交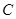 于A,B两点.若AB的中点坐标的纵坐标为
于A,B两点.若AB的中点坐标的纵坐标为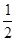 ,求
,求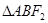 的面积.
的面积.
(本小题满分13分)已知函数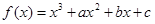 (其中,
(其中,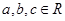 ),
),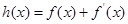 为奇函数,
为奇函数,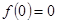 .
.
(Ⅰ)求函数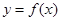 的解析式;
的解析式;
(Ⅱ)求函数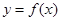 在
在 上的最值.
上的最值.