（本小题满分14分）椭圆
，椭圆的左、右焦点分别为
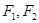,椭圆上的点到中心的最短距离为
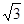，且椭圆上的点到左焦点
的最长距离为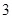
．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）若直线
交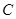
于A，B两点．若AB的中点坐标的纵坐标为
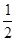，求
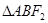的面积．
(本题满分12分)已知
都是正数，且
求
的最小值.
(本题满分12分)
已知函数
,（1）求函数
极值.（2）求函数在
上的最大值和最小值.
(本题满分12分)
已知m
,复数z=
.
（Ⅰ）实数m取什么值时？复数z为实数、纯虚数.
（Ⅱ）实数m取值范围是什么时？复数z对应的点在第四象限.
如图，在矩形ABCD中，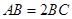
，
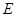为
上一点，以直线EC为折线将点B折起至点P，并保持∠PEB为锐角，连结PA、PC、PD，取PD的中点F，若有AF∥平面PEC。
（Ⅰ）试确定点E的位置；
（Ⅱ）若异面直线PE、CD所成的角为60°，求证：平面PEC⊥平面AECD。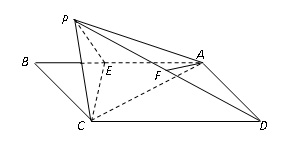
已知定义在R上的函数f(x) 同时满足：①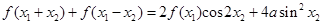
（
R，a为常数）；②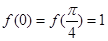
；③当
时，
≤2。
求：（Ⅰ）函数
的解析式；（Ⅱ）常数a的取值范围。