在△ABC中, BC=m2-n2,AC=2mn,AB=m2+n2(m>n),
求证:△ABC是直角三角形。
“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方
km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方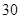 m处,过了2s后,测得小汽车与车速检测仪间距离为
m处,过了2s后,测得小汽车与车速检测仪间距离为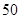 m,这辆小汽车超速了吗?
m,这辆小汽车超速了吗?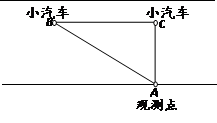
有一根高为16米的电线杆在A处断裂,如图所示,电线杆顶部C落到离电线杆底部B8m远的地方,求电线杆的断裂处A离地面有多高?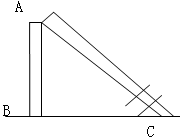
如图所示,铁路上有A、B两点(看做直线上两点)相距40千米,C、D为两村庄(看做两个点),AD⊥AB,BC垂直AB,垂足分别为A、B,AD=24千米,BC=16千米,现在要在铁路旁修建一个煤栈,使得C、D两村到煤栈的距离相等,问煤栈应建在距A点多少千米处?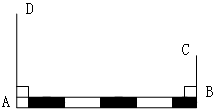
如图,小李准备建一个蔬菜大棚,棚宽4m,高3m,长20m,棚的斜面用塑料薄膜遮盖,不计强的厚度,请计算阳光透过的最大面积。