下表是初三某班女生的体重检查结果:
| 体重(kg) |
34 |
35 |
38 |
40 |
42 |
45 |
50 |
| 人数 |
1 |
2 |
5 |
5 |
4 |
2 |
1 |
根据表中信息,回答下列问题:
(1)该班女生体重的中位数是 ;
(2)该班女生的平均体重是 kg;
(3)根据上表中的数据补全条形统计图.
如图,已知AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O
切线,交OD的延长线于点E,连结BE.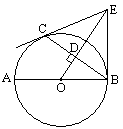
(1)求证:BE与⊙O相切;
(2)连结AD并延长交BE于点F,若OB=6,且sin∠ABC= ,求BF的长.
,求BF的长.
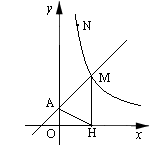
如图,直线 与y轴交于A点,与反比例函数
与y轴交于A点,与反比例函数 (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO= .
. 
(1)求k的值;
(2)设点N(1,a)是反比例函数 (x>0)图像上的点,在y轴上是否存在点P,使得PM+PN最小,若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图像上的点,在y轴上是否存在点P,使得PM+PN最小,若存在,求出点P的坐标;若不存在,请说明理由.
按要求作图并回答:
用刻度尺作线段AC (AC=5cm),以A为圆心,a为半径作圆,再以C为圆心,b为半径作圆 (其中a<5,b<5, 且要求⊙A与⊙C交于B、D两点),连结BD.
(1)若能作出满足要求的两圆,则a、b应满足的条件是.
(2)求证:AC⊥BD.
航模小组同学要在一个矩形材料AECF中剪出如图阴影所示的梯形制作机翼,请你根据图中的数据计算出BE、CD的长度以及梯形ABCD的面积(精确到个位,取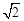 ≈1.4,
≈1.4, ≈1.7).
≈1.7).
《九章算术》第九章的第九题为:今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何.译成现代文并配图如下:圆木埋在壁中,不知大小,用锯子来锯它,锯到深度CD= cm时,量得锯痕AB=
cm时,量得锯痕AB= cm,问圆木的直径是多少cm?
cm,问圆木的直径是多少cm?