(本小题满分14分) 已知函数 .
.
(1)若函数 与
与 的图象在公共点P处有相同的切线,求实数
的图象在公共点P处有相同的切线,求实数 的值并求点P的坐标;(2)若函数
的值并求点P的坐标;(2)若函数 与
与 的图象有两个不同的交点M、N,求
的图象有两个不同的交点M、N,求 的取值范围;(3)在(Ⅱ)的条件下,过线段MN的中点作
的取值范围;(3)在(Ⅱ)的条件下,过线段MN的中点作 轴的垂线分别与
轴的垂线分别与 的图像和
的图像和 的图像交S、T点,以S为切点作
的图像交S、T点,以S为切点作 的切线
的切线 ,以T为切点作
,以T为切点作 的切线
的切线 .是否存在实数
.是否存在实数 使得
使得

 ,如果存在,求出
,如果存在,求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
(本小题满分14分) 已知函数f (x)=ex-k-x,其中x∈R. (1)当k=0时,若g(x)= 定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
定义域为R,求实数m的取值范围;(2)给出定理:若函数f (x)在[a,b]上连续,且f (a)·f (b)<0,则函数y=f (x)在区间(a,b)内有零点,即存在x0∈(a,b),使f (x0)=0;运用此定理,试判断当k>1时,函数f (x)在(k,2k)内是否存在零点.
(本小题满分13分) 近段时间我国北方严重缺水, 某城市曾一度取消洗车行业. 时间久了,车 容影响了市容市貌. 今年该市决定引进一
容影响了市容市貌. 今年该市决定引进一 种高科技产品污水净化器,允许洗车行开始营业,规定洗车行必须购买这种污水净化器,使用净化后的污水(达到生活用水标准)洗车. 污水净化器的价格是每台90万元,全市统一洗车价格为每辆每次8元. 该市今年的汽车总量是80000辆,预计今后每年汽车数量将增加2000辆.洗车行A经过测算,如果全市的汽车总量是x,那么一年内在该洗车行洗车的平均辆次是
种高科技产品污水净化器,允许洗车行开始营业,规定洗车行必须购买这种污水净化器,使用净化后的污水(达到生活用水标准)洗车. 污水净化器的价格是每台90万元,全市统一洗车价格为每辆每次8元. 该市今年的汽车总量是80000辆,预计今后每年汽车数量将增加2000辆.洗车行A经过测算,如果全市的汽车总量是x,那么一年内在该洗车行洗车的平均辆次是 ,该洗车行每年的其他费用是20000元. 问:洗车行A从今年开始至少经
,该洗车行每年的其他费用是20000元. 问:洗车行A从今年开始至少经 过多少年才能收回购买净化器的成本?(注:洗车行A买一台污水净化器就能满
过多少年才能收回购买净化器的成本?(注:洗车行A买一台污水净化器就能满 足洗车净水需求)
足洗车净水需求)
(本小题满分13分)在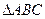 中,角
中,角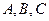 的对边分别为
的对边分别为 ,且
,且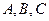 成等差数列。(1)若
成等差数列。(1)若 ,且
,且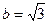 ,求
,求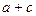 的值;(2)求
的值;(2)求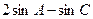 的取值范围。
的取值范围。
(本小题满分13分)若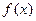 是定义在
是定义在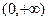 上的增函数,且对一切
上的增函数,且对一切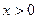 满足
满足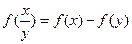 .(1)求
.(1)求 的值;(2)若
的值;(2)若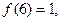 解不等式
解不等式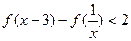 .
.