已知直线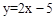
与x轴和y轴分别交于点A和点B，抛物线
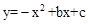的顶点M在直线AB上，且抛物线与直线AB的另一个交点为N．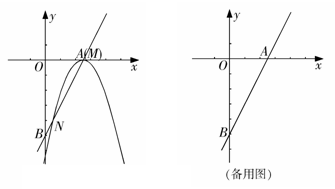
（1）如图，当点M与点A重合时，求：
①抛物线的解析式；
②点N的坐标和线段MN的长；
（2）抛物线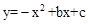在直线AB上平移，是否存在点M，使得△OMN与△AOB相似？若存在，直接写出点M的坐标；若不存在，请说明理由．
如图，矩形ABCD中，AB=8，AD=10.
（1）求矩形ABCD的周长；
（2）E是CD上的点，将△ADE沿折痕AE折叠,使点D落在BC边上点F处.
①求DE的长；
②点P是线段CB延长线上的点，连接PA，若△PAF是等腰三角形，求PB的长.
（3）M是AD上的动点，在DC 上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处, 求线段CT长度的最大值与最小值之和。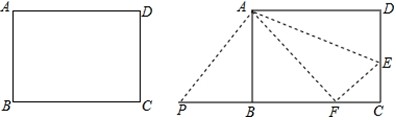
如图，长为2，宽为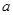
的矩形纸片（
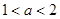），剪去一个边长等于矩形宽度的正方形（称为第一次操作）；
（1）第一次操作后剩下的矩形长为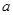，宽为；
（2）再把第一次操作后剩下的矩形剪去一个边长等于此时矩形宽度的正方形（称为第二次操作）；如此反复操作下去．
①求第二次操作后剩下的矩形的面积；
②若在第3次操作后，剩下的图形恰好是正方形，求的值．
如图，在△ABC中，∠ACB=90°，∠A=30°，BC=2．将△ABC绕点C按顺时针方向旋转
度后得到△EDC，此时点D在AB边上，斜边DE交AC边于点F.
（1）求DC的长和旋转的角度；
（2）求图中阴影部分的面积.
如图，Rt△ABC中，∠ACB=90°，AC=3，AB=5，将△ABC沿AB边所在直线向右平移3个单位，记平移后的对应三角形为△DEF，
（1）求DB的长；
（2）求此时梯形CAEF的面积．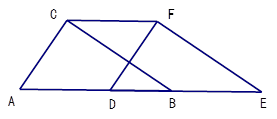
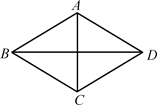
已知：菱形ABCD的两条对角线AC与BD相交于点O，且AC=6,BD=8，求菱形的周长和面积．