如图，在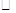
OABC中，点A在x轴上，∠AOC=60o，OC=4cm．OA=8cm．动点P从点O出发，以1cm／s的速度沿线段OA→AB运动；动点Q同时从点O出发，以acm／s的速度沿线段OC→CB运动，其中一点先到达终点B时，另一点也随之停止运动．设运动时间为t秒．
(1)填空：点C的坐标是(______，______)，对角线OB的长度是_______cm；
(2)当a=1时，设△OPQ的面积为S，求S与t的函数关系式，并直接写出当t为何值时，S的值最大?
(3)当点P在OA边上，点Q在CB边上时，线段PQ与对角线OB交于点M.若以O、M、P为顶点的三角形与△OAB相似，求a与t的函数关系式，并直接写出t的取值范围．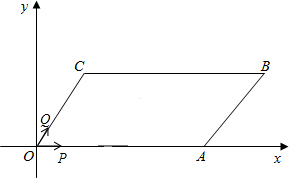
(8分)如图，AM切⊙O于点A，BD⊥AM于点D，BD交⊙O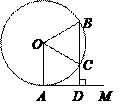
于点C，OC平分∠AOB．求∠B的度数．
(9分)某中学学生为了解该校学生喜欢球类活动的情况，随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类)，并将调查的结果绘制成如下的两幅不完整的统计图．
请根据图中提供的信息，解答下面的问题：
(1)参加调查的学生共有 人，在扇形图中，表示“其他球类”的扇形的圆心角为 度；
(2)将条形图补充完整；
(3)若该校有2000名学生，则估计喜欢“篮球”的学生共有 人．
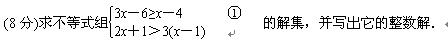
(12分)已知A(1，0)、B(0，－1)、C(－1，2)、D(2，－1)、E(4，2)五个点，抛物线y＝a(x－1)2＋k(a＞0)经过其中的三个点．
(1)求证：C、E两点不可能同时在抛物线y＝a(x－1)2＋k(a＞0)上；
(2)点A在抛物线y＝a(x－1)2＋k(a＞0)上吗？为什么？
(3)求a和k的值．