如图,直线AB交x轴于点B(4,0),交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°.
(1)直接写出直线AB的解析式;
(2)求点D的坐标;
(3)若点P是线段MB上的动点,过点P作x轴的垂线,交AB于点F,交过O、D、B三点的抛物线于点E,连接CE.是否存在点P,使△BPF与△FCE相似?若存在,请求出点P的坐标;若不存在,请说明理由.
先化简,再求值: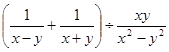 ,其中
,其中 ,
,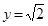 .
.
如图,ABC中,∠A=90º,AB=2㎝,AC=4㎝,动点P从点A出发,沿AB方向以1㎝/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1㎝s的速度向带你A运动,当点P到达点B时,P、Q两点同时停止运动.以AP为一边向上作正方形APDE,过点Q作QF∥BC,交AC于点F,设点P的运动时间为t s,正方形APDE和梯形BCFQ重合部分的面积为S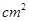 .
.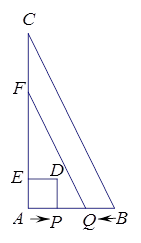
(1)当t= s时,点P与点Q重合;
(2)当t= s时,点D在QF上;
(3)当点P在Q、B两点之间(不包括Q、B两点)时,求S与t之间的函数关系式.
已知:点(1,3)在函数 的图象上,矩形ABCD的边BC在
的图象上,矩形ABCD的边BC在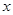 轴上,E是对角线BD的中点,函数
轴上,E是对角线BD的中点,函数 的图象又经过A,E两点,点E的横坐标为m,解答下列问题:
的图象又经过A,E两点,点E的横坐标为m,解答下列问题:
(1)求k的值;
(2)求点C的横坐标(用m表示)
(3)当∠ABD=45º时,求m的值.
正方形ABCD与正方形CEFG的位置如图所示,点G在线段CD或CD的延长线上,分别连接BD、BF、FD,得到 BFD.
BFD.
(1)在图1、图2、图3中,若正方形CEFG的边长分别为1、3、4,且正方形ABCD的边长均为3,请通过计算填写下表: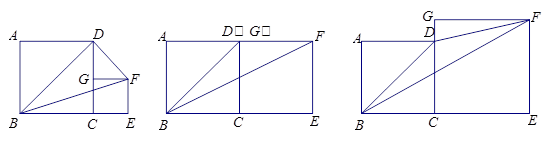
图1图2图3
| 正方形CEFG的边长 |
1 |
3 |
4 |
 BFD的面积 BFD的面积 |
(2)若正方形CEFG的边长为 ,正方形ABCD的边长为
,正方形ABCD的边长为 ,猜想
,猜想 的大小,并结合图3证明你的猜想.
的大小,并结合图3证明你的猜想.
已知:甲、乙两车分别从相距300km的A,B两地同时出发相向而行,甲到B地后立即返回,下图是它们离各自出发地的距离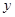 与行驶时间
与行驶时间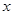 之间的函数图象.
之间的函数图象.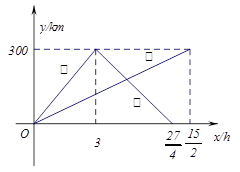
(1)请直接写出甲、乙两车离各自出发地的距离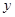 与行驶时间
与行驶时间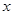 之间的函数关系式,并标明自变量
之间的函数关系式,并标明自变量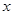 的取值范围;
的取值范围;
(2)它们在行驶过程中有几次相遇?并求出每次相遇的时间.