(本小题满分12分)袋中装有35个球,每个球上都标有1到35的一个号码,设号码为n的球重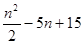 克,这些球等可能地从袋中被取出.
克,这些球等可能地从袋中被取出.
(1)如果任取1球,试求其重量大于号码数的概率;
(2)如果不放回任意取出2球,试求它们重量相等的概率;
(3)如果取出一球,当它的重量大于号码数,则放回,搅拌均匀后重取;当它的重量小于号码数时,则停止取球.按照以上规则,最多取球3次,设停止之前取球次数为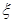 ,求E
,求E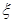 .
.
已知点 是离心率为
是离心率为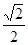 的椭圆C:
的椭圆C: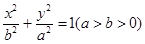 上的一点。斜率为
上的一点。斜率为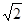 直线BD交椭圆C于B、D两点,且A、B、D三点不重合。
直线BD交椭圆C于B、D两点,且A、B、D三点不重合。
(Ⅰ)求椭圆C的方程;
(Ⅱ) 面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由?
面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由?
已知向量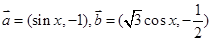 ,函数
,函数 .
.
(Ⅰ)求函数 的最小正周期
的最小正周期 ;
;
(Ⅱ)已知 、
、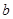 、
、 分别为
分别为 内角
内角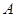 、
、 、
、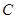 的对边, 其中
的对边, 其中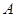 为锐角,
为锐角,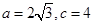 ,且
,且 ,求
,求 和
和 的面积
的面积
如图,已知四棱锥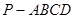 中,底面
中,底面 是直角梯形,
是直角梯形, ,
,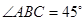 ,
,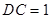 ,
, ,
, 平面
平面 ,
,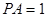 .
.
(Ⅰ)求证: 平面
平面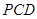 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)若 是
是 的中点,求三棱锥
的中点,求三棱锥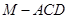 的体积.
的体积.
已知数列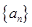 的前
的前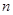 项和是
项和是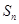 ,且
,且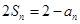 .
.
(Ⅰ)求数列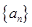 的通项公式;
的通项公式;
(Ⅱ)记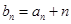 ,求数列
,求数列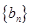 的前
的前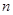 项和
项和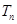
已知集合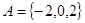 ,
,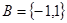 .
.
(Ⅰ)若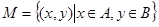 ,用列举法表示集合
,用列举法表示集合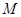 ;
;
(Ⅱ)在(Ⅰ)中的集合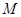 内,随机取出一个元素
内,随机取出一个元素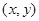 ,求以
,求以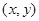 为坐标的点位于区域D:
为坐标的点位于区域D: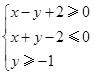 内的概率.
内的概率.