如图所示，已知抛物线的顶点为坐标原点O，矩形ABCD的顶点A，D在抛物线上，且AD平行x轴，交y轴于点F，AB的中点E在x轴上，B点的坐标为（2，1），点P（a，b）在抛物线上运动．（点P异于点O）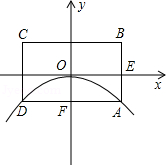
（1）求此抛物线的解析式．
（2）过点P作CB所在直线的垂线，垂足为点R，
①求证：PF=PR；
②是否存在点P，使得△PFR为等边三角形？若存在，求出点P的坐标；若不存在，请说明理由；
③延长PF交抛物线于另一点Q，过Q作BC所在直线的垂线，垂足为S，试判断△RSF的形状．
如图所示，AC为⊙O的直径且PA⊥AC，BC是⊙O的一条弦，直线PB交直线AC于点D， 
．
（1）求证：直线PB是⊙O的切线；
（2）求tan∠BCA的值
如图，根据图中数据完成填空，再按要求答题：
sin2A1+sin2B1=； sin2A2+sin2B2=； sin2A3+sin2B3=．
（1）观察上述等式，猜想：在Rt△ABC中，∠C=90°，都有sin2A+sin2B=．
（2）如图④，在Rt△ABC中，∠C=90°，∠A、∠B、∠C的对边分别是a、b、c，利用三角函数的定义和勾股定理，证明你的猜想．
（3）已知：∠A+∠B=90°，且sinA=
，求sinB．
（本小题满分１4分）如图，在平面直角坐标系
中，抛物线
过点
（0，4）和
（8，0），P（t，0）是
轴正半轴上的一个动点，M是线段AP的中点，将线段MP绕点P顺时针旋转90°得线段PB．过点B作轴的垂线、过点A作
轴的垂线，两直线相交于点D．
（1）求此抛物线的对称轴；
（2）当
为何值时，点D落在抛物线上？
（3）是否存在，使得以A、B、D为顶点的三角形与△PEB相似？若存在，求此时的值；若不存在，请说明理由．
（本小题满分１4分）如本题图①，在△ABC中，已知
．过点A作BC的平行线与∠ABC的平分线交于点D，连接CD．
（1）求
的大小；
（2）在线段
的延长线上取一点
，以
为角的一边作
，另一边交BD延长线于点E， 若、
（如本题图②所示），试求
的值（用含
的代数式表示）．
（本小题满分１2分）如图，
中，
，
．
（1）动手操作：利用尺规作以
为直径的⊙
，并标出⊙与
的交点
，与
的交点
（保留作图痕迹，不写作法）．
（2）综合应用：在你所作的圆中，求证：
；
（3）求
的周长．