某海滨浴场的岸边可以近似的看成直线，位于岸边A处的救生员发现海
中B处有人求救，救生员没有直接从A处游向B处，而是沿岸边自A跑到距离B最近的D
处，然后游向B处.若救生员在岸边的行进速度是6米/秒，在海中的行进速度是2米/秒.
（不考虑水流速度等因素）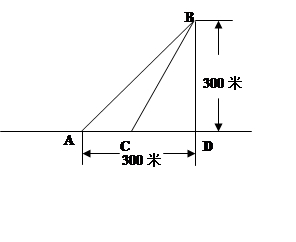
（1）请分析救生员的选择是否正确；
（2）在AD上找一点C，使救生员从A到B的时间最短，并求出最短时间.
已知几何体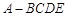
的三视图如图所示，其中俯视图和侧视图都是腰长为4的等腰直角三角形，正视图为直角梯形．
（Ⅰ）求此几何体的体积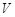
的大小；
（Ⅱ）求异面直线DE与AB所成角的余弦值；
（Ⅲ）求二面角A-ED-B的正弦值．
两仓库分别有编织袋50万个和30万个，由于抗洪抢险的需要，现需调运40万个到甲地，20万个到乙地．已知从
仓库调运到甲、乙两地的运费分别为120元/万个、180元/万个；从
仓库调运到甲、乙两地的运费分别为100元/万个、150元/万个．问如何调运，能使总运费最小？总运费的最小值是多少？
已知直线方程为
，其中
（1）求证：直线恒过定点；
（2）当
变化时，求点
到直线的距离的最大值；
（3）若直线分别与
轴、
轴的负半轴交于
两点，求
面积的最小值及此时的直线方程．
在△
中，
所对的边分别为
，
,
．
（1）求
；
（2）若
,求
．21世纪教育
设公差不为0的等差数列
的首项为1，且
构成等比数列．
（Ⅰ）求数列的通项公式；
（Ⅱ）若数列
满足
…
1－
，n∈N*，求的前n项和
．