如果我们把四个都是直角三角形的四面体称为“三节棍体”,那么从长方体八个顶点中任取四个顶点,则这四个顶点是“三节棍体”的四个顶点的概率是
A. |
B. |
C. |
D. |
用数学归纳法证明不等式“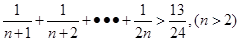 ”的过程中,由n=k到n=k+1时,不等式的左边()
”的过程中,由n=k到n=k+1时,不等式的左边()
A.增加了一项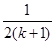 |
B.增加了两项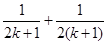 |
C.增加了一项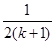 ,又减少了一项 ,又减少了一项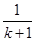 |
D.增加了两项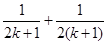 ,又减少了一项 ,又减少了一项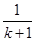 |
用反证法证明命题:“ ,且
,且 ,则
,则 中至少有一个负数”时的假设为()
中至少有一个负数”时的假设为()
A. 中至少有一个正数 中至少有一个正数 |
B. 中全为正数 中全为正数 |
C. 全都大于或等于 全都大于或等于 |
D. 中至多有一个负数 中至多有一个负数 |
有一段“三段论”推理是这样的:对于可导函数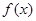 ,如果
,如果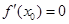 ,那么
,那么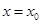 是函数
是函数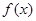 的极值点,因为函数
的极值点,因为函数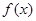 =
=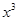 在x=0处的导数值
在x=0处的导数值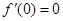 ,所以x=0是函数
,所以x=0是函数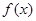 =
=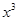 的极值点。以上推理中()
的极值点。以上推理中()
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.结论正确 |
下面几种推理过程是演绎推理的是()
A.两条直线平行,同旁内角互补;如果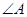 和 和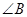 是两条直线平行的同旁内角,则 是两条直线平行的同旁内角,则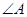 + +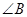 = =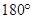 。 。 |
| B.由平面三角形的性质,推测空间四面体的性质。 |
| C.某校高二共有10个班,1班有51人,2班有53人,3班有52人,由此推测各班都超过50人。 |
D.在数列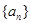 中, 中,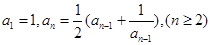 ,由 ,由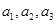 推测 推测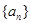 的通项公式。 的通项公式。 |
若复数Z满足Z(4-i)=5+3i(i是虚数单位),则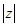 =()
=()
| A.1 | B.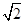 |
C.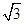 |
D.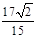 |