阅读:如图,CE∥AB,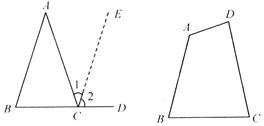
∴∠1=∠A,∠2=∠B.
∴∠ACD=∠1+∠2=∠A+∠B,这是一个有用的事实,请用这个事实,在如图5-102四边形ABCD内引一条和边平行的直线,求出∠A+∠B+∠C+∠D的度数.
(本题6分)点P、Q分别是边长为4cm的等边△ABC的边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都是1cm/s.
(1)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;
(2)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠CMQ变化吗?若变化,则说明理由,若不变,请求出它的度数.
(本题6分)某校把一块形状为直角三角形的废地开辟为生物园,如图所示,∠ACB=90°,AC=80米,BC=60米,若线段CD是一条小渠,且D点在边AB上,已知水渠的造价为10元/米,问D点在距A点多远处时,水渠的造价最低?最低造价是多少?
(本题5分)如图,已知AB=AC,AD=AE.求证:BD=CE.
(本题6分)如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.
(1)求∠DAC的度数;
(2)请说明:AB=CD.
(本题5分)尺规作图:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵桂花树.如图,要求桂花树的位置(视为点P),到花坛的两边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种桂花树的位置点P(不写作法,保留作图痕迹).