（本题6分）如图，在△ABC中，AB=AC，D为BC边上一点，∠B=30°，∠DAB=45°．
（1）求∠DAC的度数；
（2）请说明：AB=CD．
某市体育中考现场考试内容有三项：50米跑为必测项目；另外在立定跳远和实心球中选一项，在坐位体前屈和1分钟跳绳中选一项．
（1）每位考生有__________种选择方案；
（2）若用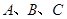
……等字母分别表示上述各种方案，请用画树状图或列表的方法求小明与小刚选择同一种方案的概率．
（1）如图，点A、B、C、D在同一条直线上，BE∥DF，∠A=∠F，AB=FD.求证：AE=FC.
（2）如图，在梯形ABCD中，AD∥BC，∠B＝90°，AD＝2，BC＝5，tanC＝
,求腰AB的长.
（1）化简：
（2）解方程组：
如图，已知抛物线y＝x2＋bx＋c经过A(-1, 0)、B(4, 5)两点，过点B作BC⊥x轴，垂足为C．
（1）求抛物线的解析式；
（2）求tan∠ABO的值；
（3）点M是抛物线上的一个点，直线MN平行于y轴交直线AB于N，如果以M、N、B、C为顶点的四边形是平行四边形，求出点M的横坐标．
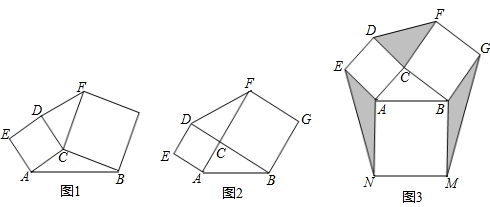
如图1，若分别以△ABC的AC、BC两边为边向外侧作的四边形ACDE和BCFG为正方形，则称这两个正方形为外展双叶正方形．
（1）发现：如图2，当∠C=90°时，求证：△ABC与△DCF的面积相等．
（2）引申：如果∠C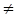
90°时，（1）中结论还成立吗？若成立，请结合图1给出证明；若不成立，请说明理由；
（3）运用：如图3，分别以△ABC的三边为边向外侧作的四边形ACDE、BCFG和ABMN为正方形，则称这三个正方形为外展三叶正方形．已知△ABC中，AC=3，BC=4．当∠C=_____度时，图中阴影部分的面积和有最大值是________．