如图,已知直线m∥n,A、B为直线n上两点,C、D为直线m上两点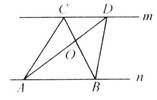
(1)请写出图中面积相等的三角形;
(2)如果A、B、C为三个定点,点D在m上移动,那么,无论D点移动到任何位置,总有___________与△ABC的面积相等,理由是:________________________.
第33个国际禁毒日到来之际,贵阳市策划了以“健康人生 绿色无毒”为主题的禁毒宣传月活动,某班开展了此项活动的知识竞赛.学习委员为班级购买奖品后与生活委员对话如下:

(1)请用方程的知识帮助学习委员计算一下,为什么说学习委员搞错了;
(2)学习委员连忙拿出发票,发现的确错了,因为他还买了一本笔记本,但笔记本的单价已模糊不清,只能辨认出单价是小于10元的整数,那么笔记本的单价可能是多少元?
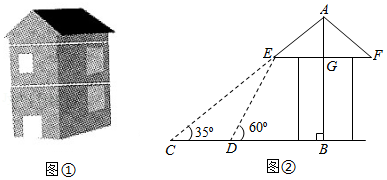
脱贫攻坚工作让老百姓过上了幸福的生活.如图①是政府给贫困户新建的房屋,如图②是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高 所在的直线,为了测量房屋的高度,在地面上 点测得屋顶 的仰角为 ,此时地面上 点、屋檐上 点、屋顶上 点三点恰好共线,继续向房屋方向走 到达点 时,又测得屋檐 点的仰角为 ,房屋的顶层横梁 , , 交 于点 (点 , , 在同一水平线上).(参考数据: , , ,
(1)求屋顶到横梁的距离 ;
(2)求房屋的高 (结果精确到 .
“2020第二届贵阳市应急科普知识大赛”的比赛中有一个抽奖活动,规则是:准备3张大小一样,背面完全相同的卡片,3张卡片的正面所写内容分别是《消防知识手册》《辞海》《辞海》,将它们背面朝上洗匀后任意抽出一张,抽到卡片后可以免费领取卡片上相应的书籍.
(1)在上面的活动中,如果从中随机抽出一张卡片,记下内容后不放回,再随机抽出一张卡片,请用列表或画树状图的方法,求恰好抽到2张卡片都是《辞海》的概率;
(2)再添加几张和原来一样的《消防知识手册》卡片,将所有卡片背面朝上洗匀后,任意抽出一张,使得抽到《消防知识手册》卡片的概率为 ,那么应添加多少张《消防知识手册》卡片?请说明理由.
如图,一次函数 的图象与反比例函数 的图象相交,其中一个交点的横坐标是2.
(1)求反比例函数的表达式;
(2)将一次函数 的图象向下平移2个单位,求平移后的图象与反比例函数 图象的交点坐标;
(3)直接写出一个一次函数,使其过点 ,且与反比例函数 的图象没有公共点.

如图,四边形 是矩形, 是 边上一点,点 在 的延长线上,且 .
(1)求证:四边形 是平行四边形;
(2)连接 ,若 , , ,求四边形 的面积.
