在数轴上表示下列各数，并比较它们的大小．
－2，0，1，1．5，
．
已知二次函数y=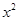
+4x+k-1．
（1）若抛物线与x轴有两个不同的交点，求k的取值范围;
（2）若抛物线的顶点在x轴上，求k的值．
如图，已知ABCD的周长为8 cm，∠B=30°，若边长AB为x cm．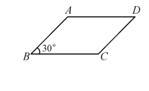
（1）写出平行四边形ABCD的面积y（cm2）与x（cm）的函数关系式，并求自变量x的取值范围．
（2）当x取什么值时，y的值最大？并求出最大值．
已知二次函数y=
+4．
（1）写出抛物线的开口方向、顶点坐标和对称轴．
（2）画出此函数的图象，并说出此函数图象与y=
的图象的关系．
已知函数y=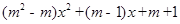
（1）若这个函数是一次函数，求m的值;
（2）若这个函数是二次函数，则m的值应怎样？
